7. Time Evolution in Phase Space: Poisson Brackets and Constants of the Motion
The Poisson Bracket
A function
of
the phase space coordinates of the system and time has total time derivative
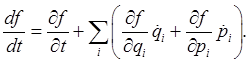
This is often written as
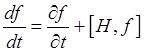
where
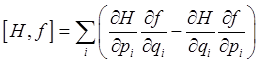
is called the Poisson bracket. (Warning! This is Landau's definition: many others use the opposite sign.)
If, for a phase space function 
(that is, no
explicit time dependence) 
then is a constant of
the motion, also called an integral of the motion.
In fact, the Poisson bracket can be defined for any two functions defined in phase space:
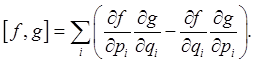
It's straightforward to check the following properties of the Poisson bracket:
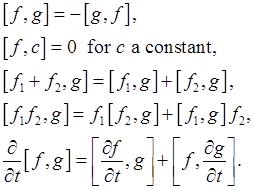
The Poisson brackets of the basic variables are easily found to be:
Now, using 
and
the basic variable P.B.'s, 
and, in fact,
the bracket of
with
any reasonably smooth function of
is:
Interlude: a Bit of History of Quantum Mechanics
It should be clear at this point that the Poisson bracket is
very closely related to the commutator in quantum mechanics. In the usual
quantum mechanical notation, the momentum operator 
so the commutator
(which acts on a wave function, remember)
identical to the Poisson bracket result multiplied by the
constant 
The first successful mathematical formulation of quantum
mechanics, in 1925 (before Schrodinger's equation!) was by Heisenberg. As you
know, he was the guy with the Uncertainty Principle: he realized that you
couldn't measure momentum and position of anything simultaneously. He
represented the states of a quantum system as vectors in some Hilbert space,
and the dynamical variables as matrices acting on these vectors. He
interpreted the result of a measurement as finding an eigenvalue of a matrix.
If two variables couldn't be measured at the same time, the matrices had a
nonzero commutator. In particular, for a particle's position and momentum the
matrix representations satisfied 
Dirac made the connection with Poisson brackets on a long
Sunday walk, mulling over Heisenberg's 
(as it was
written). He suddenly but dimly remembered what he called "these strange
quantities" -- the Poisson brackets -- which he felt might have properties
corresponding to the quantum mathematical formalism Heisenberg was building.
But he didn't have access to advanced dynamics books until the college library
opened the next morning, so he spent a sleepless night. First thing Monday, he
read the relevant bit of Whittaker's Analytical Dynamics, and saw he was
correct. (From the biography by Helge Kragh.)
Dirac went on to adapt the equation 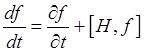to quantum
mechanics: for time-independent functions,
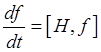, becomes 
for time development of an operator in the Heisenberg picture, where state vectors of closed systems do not vary in time (as opposed to the Schrodinger picture, where the vectors vary and the operators remain constant).
The Jacobi Identity
Another important identity satisfied by the Poisson brackets is the Jacobi identity
This can be proved by the incredibly tedious method of just
working it out. A more thoughtful proof is presented by Landau, but we're not
going through it here. Ironically, the Jacobi identity is a lot easier to
prove in its quantum mechanical incarnation (where the bracket just signifies
the commutator of two matrix operators, 
).
Jacobi's identity plays an important role in general relativity.
Poisson's Theorem
If
are
two constants of the motion (meaning they both have zero Poisson brackets with
the Hamiltonian), then the Poisson bracket 
is also a
constant of the motion. Of course, it could be trivial, like 
or it could be a
function of the original variables. But sometimes it's a new constant of
motion. Ifare
time-independent, the proof follows immediately from Jacobi's identity. A
proof for time dependent functions is given in Landau -- it's not
difficult.
Example: angular momentum components
A moving particle has angular momentum about the origin
so
Using the Poisson brackets found above,
we have
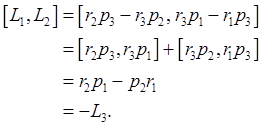
We conclude that if two components of angular momentum are conserved, so is the third.
(Note: we remind the reader that we are following Landau's convention, in which the Poisson brackets have the opposite sign to the more common use, for example in Goldstein and Wikipedia.)
previous home next PDF