Due: October 31, 1995
Due: October 31, 1995

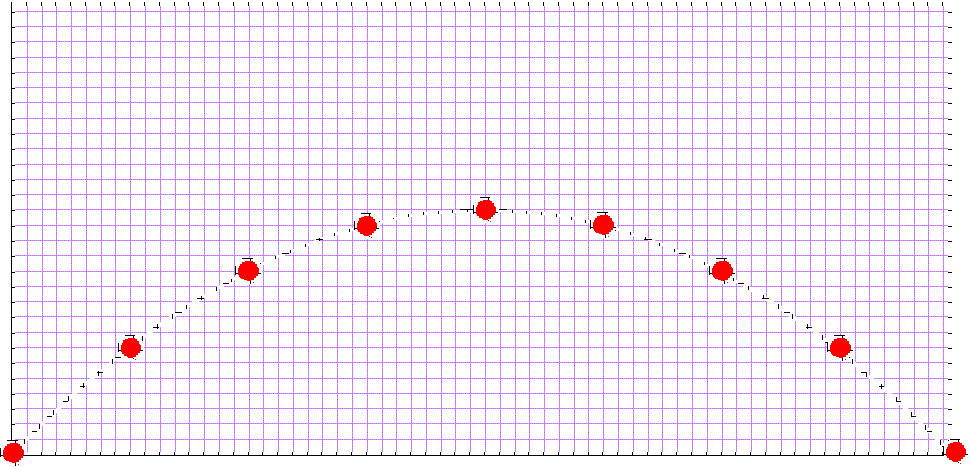
1. The above picture represents the flight of a ball thrown into the air (although air resistance effects have been neglected). The background grid is in one-foot squares. The blobs represent the position of the ball at successive quarter-second intervals.
(a) By counting lines, find the average horizontal velocity of the ball, in feet per second, during the first quarter of a second.
(b) By reviewing the whole picture, find how the horizontal velocity (in feet per second) varies throughout the flight.
(c) By counting squares, find the average vertical velocity of the ball during the first quarter of a second.
(d) Make a table of the ball's average vertical velocity for all eight quarter-second periods in the flight. Count velocity upwards as positive, downwards as negative.
(e) Plot a graph of velocity (on the y-axis) as a function of time (on the x-axis) for the whole flight.
(f) Acceleration is rate of change of velocity. It is measured here in feet per second per second. Plot a graph of acceleration as a function of time for the whole flight. What can you conclude about the acceleration of the ball at the topmost point of the path?
(g) Suppose now instead that the ball had been thrown directly upwards. Would it be accelerating at the topmost point of its flight?
2. Read carefully the Simp-Salv exchange at the bottom of page 164 and top of 165 in Two New Sciences, and explain it as simply as you can in your own words.
3. For the planets Mercury, Venus, Earth, Mars, Jupiter, Saturn the distances R from the sun in tens of millions of miles are: 3.596, 6.716, 9.290, 14.16, 48.33, 88.61, and the orbital periods T in days are: 86.96, 224.7, 365.3, 687.1, 4323, 10760. Use a calculator to find for each planet the ratio R3/T2 in these units. This is the ratio Kepler said was the same for all. How close do you find them to be? What might limit the accuracy of these numbers?
4. Galileo first observed mountains on the moon in 1610. When did these mountains first make an appearance in Italian religious art? (It's on the Web).
5. John Donne put it this way:
How great love is, presence best tryall makes,
But absence tryes how long this love will bee;
To take a latitude,
Sun, or starres, are fitliest view'd
At their brightest, but to conclude
Of longitudes, what other way have wee,
But to marke when, and where the darke eclipses bee?
(I found this in Roger's Physics for the Inquiring Mind).
Apart from the merits of this analogy, what astronomical points is Donne making? This was written about 1600. When, after that, did an "other way" first appear?