Homework due Tuesday September 26, 1995
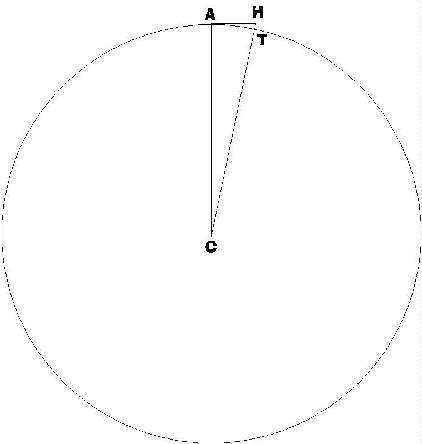 1. Here's another way to look at the "how far can we see"
problem. H and T denote your head and toes, standing on a beach.
A is the furthest you can see the surface of the (very still)
water. C is the center of the earth. AH is a tangent to the earth's
surface at A (right?), so CAH is a right angled triangle. Apply
Pythagoras' theorem to this triangle, and see if you can get the
result we found before - that is, assume HT is one-thousandth
of a mile (is it?) take the earth's diameter to be 7,900
miles, and figure out just how far you can see, before the earth's
curvature stops you.
1. Here's another way to look at the "how far can we see"
problem. H and T denote your head and toes, standing on a beach.
A is the furthest you can see the surface of the (very still)
water. C is the center of the earth. AH is a tangent to the earth's
surface at A (right?), so CAH is a right angled triangle. Apply
Pythagoras' theorem to this triangle, and see if you can get the
result we found before - that is, assume HT is one-thousandth
of a mile (is it?) take the earth's diameter to be 7,900
miles, and figure out just how far you can see, before the earth's
curvature stops you.
2. On Saturday, September 23, the sun will set exactly twelve hours after it rises in Charlottesville. For what other parts of the world will that also be true? Where in the world will the sun be exactly overhead at midday on Saturday? Describe the motion of the sun as seen in the sky from the north pole on that day. What is the angle between the vertical and a pencil pointing directly at the sun at midday in Charlottesville on Saturday? What is the latitude of Charlottesville? Are these angles related?
3. Draw an ellipse by using two thumbtacks or pins or whatever and a piece of string and a pen or pencil. Use a ruler to draw straight lines from the foci (where the pins were) to a few points on the curve and convince yourself that rays coming from one focus would reflect back to the other one on hitting the curve. What angles should be equal for this to occur? By adjusting the string length, get a long thin ellipse with the same foci.
4. Write down the squares of the negative and positive integers -4, -3, -2, -1, 0, 1, 2, 3, 4. Now make a plot, preferably on graph paper, of y = x2 by taking x to have the integer values -4 up to 4 and y to have the square values you just found. Draw a curve through all these points. It might be difficult to see how it goes near zero, so find the squares of ½ and ¼ as well and put in these extra points to guide you. This curve is a parabola. How does this relate to the long thin ellipse in problem 3?