What is Pythagoras' theorem, and how do I do this proof?
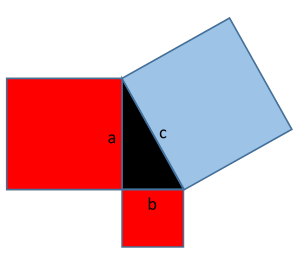
Pythagoras' theorem states that for a right-angled triangle with sides of length a, b, c, with c being the longest, the area of the square erected on that side c2 is equal to the sum of the areas of squares on the other two sides: a2+b2.
It's really about areas: Pythagoras is claiming that in the figure here, the blue area, c x c = c2, is exactly equal to the sum of the two red areas, a2+b2.
Our trick for proving this is as follows: we arrange four identical copies of our a, b, c triangle around one copy of the c x c square, as in the figure below. So the (red line) square around the whole thing has total area equal to four times the area of the original triangle, plus the area c2 of the square on the longest side.
Then we can move the four triangles around inside the big square,
 to see that the total area inside that big square equals four times the area of the triangle plus the sum of
the two areas on the other sides. Pythagoras' result then follows.
to see that the total area inside that big square equals four times the area of the triangle plus the sum of
the two areas on the other sides. Pythagoras' result then follows.
You do the moving around to discover this for yourself! (Touch and drag the triangles.)
The result doesn't depend on the triangle sides having any special lengths, only that it's a right angle triangle. Try different side lengths.