DDO: Phase Response to Driving Force
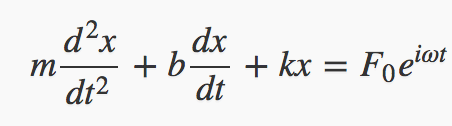
How, exactly, does the damped oscillator respond to the periodic driving force? It’s pretty clear that at low frequencies the damping will cause it to lag behind, the amplitude will peak after the force does, a phase lag. You can see this by setting omega at 0.75, damping b = 1. On starting the applet, there will be transients that die away eventually to leave the steady state. The momentary phase lag is displayed, it finally goes to the calculated steady phase lag. (Note that the momentary phase lag calculation is necessarily approximate, since the response curve is not initially at a single frequency.)
On increasing the driving omega to 1, the resonant frequency, the lag goes to 90 degrees. Look at the graph. You’ll see that at this frequency the maximum driver amplitude coincides with the maximum oscillator velocity, this means the work done by the driver is maximized.
To see clearly what happens for high frequencies, lower the damping to 0.1. The transients will now take longer to die out, but when they do, you’ll see the driver and oscillator are close to 180 degrees out of phase. Can you see why this means the driver is doing very little work?
What about the amplitude response? For small damping, it’s maximum essentially at the resonant frequency, but for large damping (try b = 1 or 2) the maximum is at a frequency lower than the resonant one. Check this out! (Pause then use the nudge buttons to find the amplitude exactly.) Could the maximum be in the limit of zero frequency?
All the math details are in my lecture here .
Program by: Carter Hedinger