Damped Driven Oscillator: Response to Different Initial Condtions
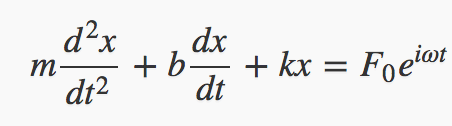
How does the behavior of a driven damped oscillator depend on the initial position and velocity? In this applet, you can set two different initial conditions and compare the curves.
To get the idea, first run it with the presets, look at the very different curves, then press the “track difference” bar and run it again.
The steady state solution of the driven damped equation (which it approaches as time passes) is completely determined by the given driving force: there are no adjustable parameters. This steady state response has the periodicity of the driving force.
However, you can always add to it a solution of the homogeneous equation (meaning the damped oscillator with no driving force), this extra term will have the periodicity of the oscillator. In fact, you have to add such a term to satisfy initial conditions (unless you’re very lucky). For nonzero damping, though, this added term will die out as time progresses, it’s a transient. The curves for different initial conditions differ by just such a transient, and they gradually move together. That’s the main point of this applet.
Here's the relevant lecture.
Program by: Carter Hedinger