Driven Damped Anharmonic Oscillator
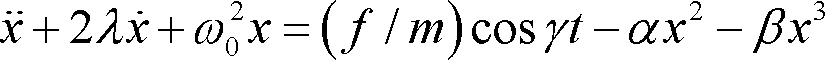
If we take a harmonic oscillator and add an x4 term, to give a potential 1⁄2x2 + 1⁄4x4,
the frequency of oscillation is just the harmonic for small swings (amplitude << 1), but for amplitudes of order one and more the steeper sides of the x4 term kick in, and the frequency goes up. (For more on this, see the previous applet
Particle in an Anharmonic Potential ).
Therefore, to drive the oscillations to large amplitude, beginning at rest, we must first drive in resonance with the harmonic term, but then as the amplitude builds up, increase our driving frequency to stay in sync.
However, when you do this, there’s a surprise: at a certain frequency, depending on the strength of the driving force, on slightly increasing the frequency (keeping everything else constant) the amplitude drops dramatically, typically by a factor of two or so, and stays there, in fact decreasing
for any further increase in frequency.
This unexpected phenomenon is explained in Landau’s book, and reproduced in my online notes. Explore it yourself using this applet.
Walk-Through: Discontinuous Response!
(Note: to check how the x4 term increases the frequency of oscillation of the undamped, undriven oscillator.
either use the previous applet, or use this one by first setting both damping term and driving term to zero. Set x = 0.1, v = 0 and press play. The graph has a frequency
readout, you’ll see it’s close to the harmonic oscillator. Then successively increase the initial displacement, and watch how the frequency increases.)
Next, we’ll look for the discontinuous amplitude change predicted by Landau.
Set ω₀2 = m = 𝛽 = 1, α = 0, 2λ = 0.34. (Or just reload the applet -- these are the default values.)
Put f = 0.5. Gradually increase γ from 1. The drop occurs around γ = 1.39.
Try now f = 0.3. The curve is now like a distorted resonance, steep on the high frequency side, but not discontinuous. Increase f. The drop sets in around
f = 0.4. This agrees pretty well with Landau’s estimate.
Here's the relevant lecture.
Next applet in this series: Driven Damped Pendulum.
Program by: Carter Hedinger