previous
index
next
Using Vectors to Describe Motion
Michael Fowler, University of Virginia
Uniform Motion in a Straight Line
Let us consider first the simple case of a car moving at a steady speed
down a straight road. Once we've agreed on the units we are using to
measure speed -- such as miles per hour or meters per second, or whatever -- a simple
number, such as 55 (mph), tells us all there is to say in describing steady
speed motion. Well, actually, this is not quite all: it doesn't tell us which way
(east or west, say) the car is moving. For some purposes, such as figuring gas
consumption, this is irrelevant, but if the aim of the trip is to get
somewhere, as opposed to just driving around, it is useful to know the
direction as well as the speed.
To convey the direction as well as the speed, physicists make a
distinction between two words that mean the same thing in everyday life: speed
and velocity.
Speed, in physics jargon, keeps its ordinary meaning: it is simply a
measure of how fast something's moving, and gives no clue about
which direction it's moving in.
Velocity, on the other hand, in physics jargon includes direction.
For motion along a straight line, velocity can be positive or negative. For a
given situation, such as Charlottesville to Richmond, we have to agree
beforehand that one particular direction, such as away from Charlottesville,
counts as positive, so motion towards Charlottesville would then always be at a
negative velocity (but, of course, a positive speed, since speed
is always positive, or zero).
Uniform Motion in a Plane
Now think about how you would describe quantitatively the motion of a smooth
ball rolling steadily on a flat smooth tabletop (so frictional effects are
negligible, and we can take the speed to be constant). Obviously, the first
thing to specify is the speed: how fast is it moving, say in meters per second?
But next, we have to tackle how to give its direction of motion, and
just positive or negative won't do, since it could be moving at any angle to
the table edge.
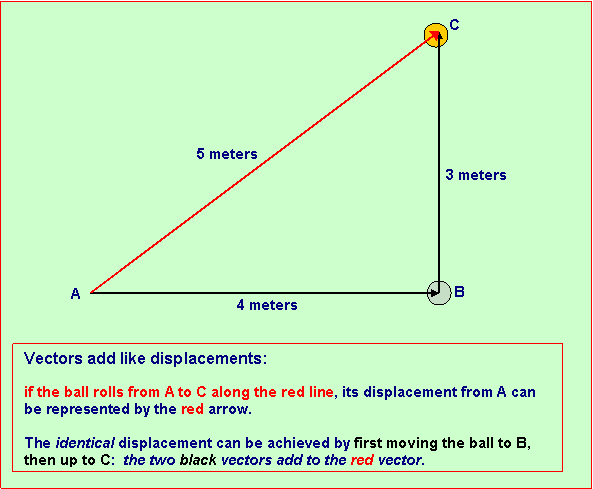
One approach to describing uniform motion in the plane is a sort of
simplified version of Galileo's "compound motion" analysis of projectiles. One
can think of the motion of the ball rolling steadily across the table as being
compounded of two motions, one a steady rolling parallel to the length
of the table, the other a steady rolling parallel to the width of the
table. For example, one could say that in its steady motion the ball is
proceeding at a steady four meters per second along the length of the table,
and, at the same time, it is proceeding at a speed of three meters per second
parallel to the width of the table (this is a big table!). To visualize what
this means, think about where the ball is at some instant, then where it is one
second later. It will have moved four meters along the length of the table,
and also three meters along the width. How far did it actually move? And in
what direction?
We can see that if the ball's uniform motion is compounded of a steady
velocity of 4 meters per second parallel to the length of the table and a
steady velocity of 3 meters per second parallel to the width, as shown above,
the actual distance the ball moves in one second is 5 meters (remembering
Pythagoras' theorem, and in particular that a right angled triangle with the
two shorter sides 3 and 4 has the longest side 5 -- we chose these numbers to make
it easy). That is to say, the speed of the ball is 5 meters per
second.
What, exactly, is its velocity? As stated above, the velocity
includes both speed and direction of motion. The simplest and
most natural way to represent direction is with an arrow. So, we represent
velocity by drawing an arrow in the plane indicating the direction the ball is
rolling in. We can see on the above representation of a table that this is the
direction of the slanting line arrow, which showed from where to where the ball
moved in one second, obviously in the direction of its velocity. Hence, we
represent the direction of the velocity by drawing an arrow pointing in that
direction.
We can make the arrow represent the speed, as well, by agreeing on a rule
for its length, such as an arrow 1 cm long corresponds to a speed of 1 meter
per second, one 2 cm long represents 2 meters per second, etc. These arrows
are usually called vectors.
Let us agree that we represent velocities for the moment by arrows pointing
in the direction of motion, and an arrow 2 cm long corresponds to a speed of 1
meter per second. Then the velocity of the ball, which is 5 meters per second
in the direction of the slanting arrow above, is in fact represented
quantitatively by that arrow, since it has the right length: 10 cms. Recalling
that we began by saying the ball had a velocity 4 meters per second parallel to
the length of the table, and 3 meters per second parallel to the width, we
notice from the figure that these individual velocities, which have to be added
together to give the total velocity, can themselves be represented by arrows
(or vectors), and, in fact, are represented by the horizontal and vertical
arrows in the figure. All we are saying here is that the arrows showing how
far the ball moves in a given direction in one second also represent its
velocity in that direction, because for uniform motion velocity just means how
far something moves in one second.
The total velocity of 5 meters per second in the direction of the dashed
arrow can then be thought of as the sum of the two velocities of 4 meters per
second parallel to the length and 3 meters per second parallel to the width.
Of course, the speeds don't add.
Staring at the figure, we see the way to add these vectors is to place
the tail of one of them at the head of the other, then the sum is given by the
vector from the other tail to the other head. In other words, putting the
two vectors together to form two sides of a triangle with the arrows pointing
around the triangle the same way, the sum of them is represented by the third
side of the triangle, but with the arrow pointing the other way.
Relative Velocities: a Child Running in a Train
As we shall see, relative velocities play an important role in relativity,
so it is important to have a clear understanding of this concept. As an
example, consider a child running at 3 meters per second (about 6 mph) in a
train. The child is running parallel to the length of the train, towards the
front, and the train is moving down the track at 30 meters per second. What is
the child's velocity relative to the ground? It is 33 meters per second in the
direction the train is moving along the track (notice we always specify direction
for a velocity). To really nail this down, you should think through just how
far the child moves relative to the ground in one second: three meters closer to
the front of the train, and the train has covered 30 meters of ground.
A trickier point arises if the child is running across the train,
from one side to the other. (This run will only last about one second!) Again,
the way to find the child's velocity relative to the ground is to visualize how
much ground the child covers in one second: three meters in the direction across
the track, from one side to the other, plus thirty meters in the direction
along the track.
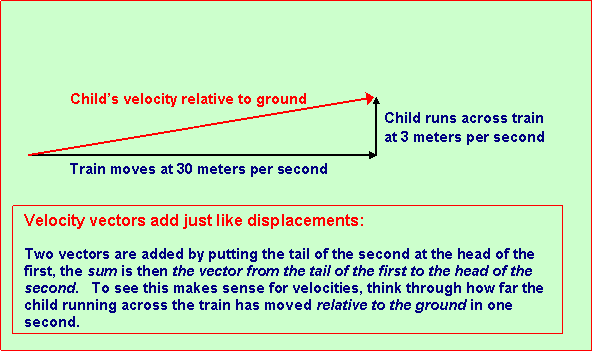
To find the total velocity, we now have to add two velocities at right
angles, using the "head to tail" rule for adding vectors. This is just the
same problem as the ball rolling across the table at an angle discussed above,
and we need to use Pythagoras' theorem to find the child's speed relative
to the ground.
Here is another example of vector addition, this time the two vectors to be
added are not perpendicular to each other, but the same rules apply:
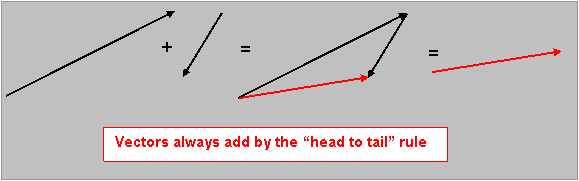
So in the diagram above, the two vectors on the left add to give the vector
on the right. To get a bit less abstract, this could represent relative
velocity in the following way: the big arrow on the left might be the speed at
which a person is swimming relative to water in a river, the little arrow is
the velocity at which the river water is moving over the river bed. then the
vector sum of these two represents the velocity of our swimmer relative to the
river bed, which is what counts for actually getting somewhere!
Exercise: Suppose you are swimming upstream at a speed relative to
the water exactly equal to the rate the water is flowing downstream, so you're
staying over the same spot on the river bed. Draw vectors representing your
velocity relative to the water, the water's velocity relative to the river bed,
and your velocity relative to the river bed. From this trivial example, if I
draw a vector A, you can immediately draw -A, the vector which
when added to A (using the rule for vector addition stated above) gives
zero.
Aristotle's Law of Horizontal Motion
We restrict our considerations here to an object, such as an oxcart, moving
in a horizontal plane. Aristotle would say (with some justification) that it
moves in the direction it's being pushed (or pulled), and with a speed proportional
to the force being applied. Let us think about that in terms of vectors. He
is saying that the magnitude of the velocity of the object is proportional to
the applied force, and the direction of the velocity is the direction of the
applied force. It seems natural to conclude that not only is the velocity a
vector, but so is the applied force! The applied force certainly has magnitude
(how hard are we pushing?) and direction, and can be represented by an arrow
(we would have to figure out some units of force if we want the length to
represent force quantitatively -- we will come back to this later). But that
isn't quite the whole story -- an essential property of vectors is that you can
add them to each other, head to tail, as described above. But if you have two
forces acting on a body, is their total effect equivalent to that of a force
represented by adding together two arrows representing the individual forces
head to tail? It turns out that if the two forces act at the same point, the
answer is yes, but this is a fact about the physical world, and needs to be
established experimentally. (It is not true in the subnuclear world, where the
forces of attraction between protons and neutrons in a nucleus are affected by
the presence of the other particles.)
So Aristotle's rule for horizontal motion is: velocity is
proportional to applied force.
This rule seems to work well for oxcarts, but doesn't make much sense for
our ball rolling across a smooth table, where, after the initial shove, there
is no applied force in the direction of motion.
Galileo's Law of Horizontal Motion
Galileo's Law of Horizontal Motion can be deduced from his statement near
the beginning of Fourth day in Two New Sciences:
Imagine any particle projected along a horizontal plane without friction;
then we know ... that this particle will move along this same plane with a
motion which is uniform and perpetual, provided the plane has no limits.
So Galileo's rule for horizontal motion is: velocity = constant,
provided no force, including friction, acts on the body.
The big advance from Aristotle here is Galileo's realization that
friction is an important part of what's going on. He knows that if there
were no friction, the ball would keep at a steady velocity. The reason Aristotle
thought it was necessary to apply a force to maintain constant velocity was
that he failed to identify the role of friction, and to realize that the force
applied to maintain constant velocity was just balancing the frictional loss.
In contrast, Galileo realized the friction acted as a drag force on the ball,
and the external force necessary to maintain constant motion just balanced this
frictional drag force, so there was no total horizontal force on the
ball.
Galileo's Law of Vertical Motion
As we have already discussed at length, Galileo's Law of Vertical Motion is:
For vertical motion: acceleration = constant (neglecting air resistance, etc.)
Describing Projectile Motion with Vectors
As an exercise in using vectors to represent velocities, consider the
velocity of a cannonball shot horizontally at 100 meters per second from the
top of a cliff: what is the velocity after 1, 2, 3 seconds? As usual, neglect
air resistance.
The initial velocity is represented by a horizontal arrow, which we take to
be 10 cms long, for convenience:

After one second, the downward velocity will have increased from zero to 10
meters per second, as usual for a falling body. Thus, to find the total
velocity after one second, we need to add to the initial velocity, the vector
above, a vertically downward vector of length 1 cm, to give the right scale:
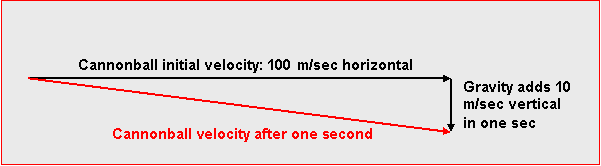
It is worth noting that although the velocity has visibly changed in this
first second, the speed has hardly changed at all -- remember the speed is
represented by the length of the slanting vector, which from Pythagoras'
theorem is the square root of 101 cms long, or about 10.05 cms, a very tiny
change. The velocity after two seconds would be given by adding two of the
dashed downward arrows head-to-tail to the initial horizontal arrow, and so on,
so that after ten seconds, if the cliff were high enough, the velocity would be
pointing downwards at an angle of 45 degrees, and the speed by this point would
have increased substantially.
Acceleration
Galileo defined naturally accelerated motion as downward motion in which
speed increased at a steady rate, giving rise to units for acceleration that
look like a misprint, such as 10 meters per second per second.
In everyday life, this is just what acceleration means: how fast something's
picking up speed.
However, in physics jargon, acceleration (like velocity) has a more subtle
meaning: the acceleration of an object is its rate of change of velocity.
From now on, this is what we mean when we say acceleration.
At first this might seem to you a nitpicking change of definition -- but it
isn't. Remember velocity is a vector. It can change without its
length changing -- it could just swing around and point in a different direction.
This means a body can accelerate without changing speed!
Why would we want to define acceleration in such a nonintuitive way? It
almost seems as if we are trying to make things difficult! It turns out that
our new definition is what Galileo might call the natural definition of
acceleration. In the true laws of motion that describe things that happen in
the universe, as we shall discuss below, if a body has a net force acting on
it, it accelerates. But it doesn't necessarily change speed -- it might just
swing its velocity around, in other words veer off in a different direction.
Therefore, as we shall see, this new definition of acceleration is what we need
to describe the real world.
For motion in a straight line, our definition is the same as Galileo's: we
agree, for example, that the acceleration of a falling body is 10 meters per
second per second downwards.
previous
index
next




