Early Greek Science: Thales to Plato
The Milesians
The first recorded important contributions to Greek science
are from the city of Miletus, near the coast of what is now Turkey, beginning with Thales in about 585 B.C., followed by Anaximander
about 555 B.C., then Anaximenes in 535 B.C. We shall
argue below that these Milesians were the first to do real science, immediately
recognizable as such to a modern scientist, 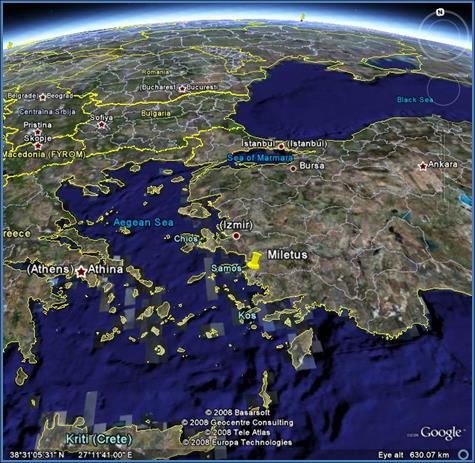 as
opposed to developing new technologies.
as
opposed to developing new technologies.
The crucial contribution of Thales to scientific thought was the discovery of nature. By this, we mean the idea that the natural phenomena we see around us are explicable in terms of matter interacting by natural laws, and are not the results of arbitrary acts by gods.
An example is Thales' theory of earthquakes, which was that the (presumed flat) earth is actually floating on a vast ocean, and disturbances in that ocean occasionally cause the earth to shake or even crack, just as they would a large boat. (Recall the Greeks were a seafaring nation.) The common Greek belief at the time was that the earthquakes were caused by the anger of Poseidon, god of the sea. Lightning was similarly the anger of Zeus. Later, Anaximander suggested lightning was caused by clouds being split up by the wind, which in fact is not far from the truth.
The main point here is that the gods are just not mentioned in analyzing these phenomena. The Milesians' view is that nature is a dynamic entity evolving in accordance with some admittedly not fully understood laws, but not being micromanaged by a bunch of gods using it to vent their anger or whatever on hapless humanity.
An essential part of the Milesians' success in developing a picture of nature was that they engaged in open, rational, critical debate about each others ideas. It was tacitly assumed that all the theories and explanations were directly competitive with one another, and all should be open to public scrutiny, so that they could be debated and judged. This is still the way scientists work. Each contribution, even that of an Einstein, depends heavily on what has gone before.
The theories of the Milesians fall into two groups:
(1) theories regarding particular phenomena or problems, of the type discussed above,
(2) speculations about the nature of the universe, and human life.
Concerning the universe, Anaximander suggested that the earth was a cylinder, and the sun, moon and stars were located on concentric rotating cylinders: the first recorded attempt at a mechanical model. He further postulated that the stars themselves were rings of fire. Again, a very bold conjecture--all heavenly bodies had previously been regarded as living gods.
He also considered the problem of the origin of life, which is of course more difficult to explain if you don't believe in gods! He suggested that the lower forms of life might be generated by the action of sunlight on moist earth. He also realized that a human baby is not self-sufficient for quite a long time, so postulated that the first humans were born from a certain type of fish.
All three of these Milesians struggled with the puzzle of the origin of the universe, what was here at the beginning, and what things are made of. Thales suggested that in the beginning there was only water, so somehow everything was made of it. Anaximander supposed that initially there was a boundless chaos, and the universe grew from this as from a seed. Anaximenes had a more sophisticated approach, to modern eyes. His suggestion was that originally there was only air (really meaning a gas) and the liquids and solids we see around us were formed by condensation. Notice that this means a simple initial state develops into our world using physical processes which were already familiar. Of course this leaves a lot to explain, but it's quite similar to the modern view.
Early Geometry
One of the most important contributions of the Greeks was their development of geometry, culminating in Euclid's Elements, a giant textbook containing all the known geometric theorems at that time (about 300 BC), presented in an elegant logical fashion.
Notice first that the word "geometry" is made up of "geo", meaning the earth, and "metry" meaning measurement of, in Greek. (The same literal translations from the Greek give geography as picturing the earth (as in graphic) and geology as knowledge about the earth. Of course, the precise meanings of all these words have changed somewhat since they were first introduced.)
The first account we have of the beginnings of geometry is from the Greek historian Herodotus, writing (in 440 B.C. or so) about the Egyptian king Sesotris (1300 B.C.):
"This king moreover (so they said) divided the country among all the Egyptians by giving each an equal square parcel of land, and made this the source of his revenue, appointing the payment of a yearly tax. And any man who was robbed by the river of a part of his land would come to Sesotris and declare what had befallen him; then the king would send men to look into it and measure the space by which the land was diminished, so that thereafter it should pay the appointed tax in proportion to the loss. From this, to my thinking, the Greeks learnt the art of measuring land..."
On the other hand Aristotle, writing a century later, had a more academic, and perhaps less plausible, theory of the rise of geometry:
"..the sciences which do not aim at giving pleasure or at the necessities of life were discovered, and first in the places where men first began to have leisure. That is why the mathematical arts were founded in Egypt, for there the priestly class was allowed to be at leisure."
However, as Thomas Heath points out in A History of Greek Mathematics, (page 122) one might imagine that if this (that is, Aristotle's theory) were true, Egyptian geometry "would have advanced beyond the purely practical stage to something more like a theory or science of geometry. But the documents which have survived do not give any grounds for this supposition; the art of geometry in the hands of the priests never seems to have advanced beyond mere routine. The most important available source of information about Egyptian mathematics is the Papyrus Rhind written probably about 1700 BC, but copied from an original of the time of King Amenemhat III (Twelfth Dynasty), say 2200 BC."
 Heath goes on to give details of what appears in this
document: areas of rectangles, trapezia and triangles, areas of circles given
as (8d/9)2, where d is the diameter, corresponding to
pi equal to 3.16 or so, about 1% off. There are approximate volume measures for
hemispherical containers, and volumes for pyramids.
Heath goes on to give details of what appears in this
document: areas of rectangles, trapezia and triangles, areas of circles given
as (8d/9)2, where d is the diameter, corresponding to
pi equal to 3.16 or so, about 1% off. There are approximate volume measures for
hemispherical containers, and volumes for pyramids.
Another important Egyptian source is the Moscow Papyrus, which includes the very practical problem of calculating the volume of a pyramid! (Actually with a flat top: look at the figure, from Wikipedia.)
A brief overview of the early history of geometry, up to Euclid, has been written by the Greek author Proclus. He asserts that geometry was first brought to Greece by Thales, after he spent some years in Egypt.
The Pythagoreans: a Cult with a Theorem, and an Irrational Discovery
Pythagoras was born about 570 B.C. on the island of Samos (on the map above), less than a hundred miles from Miletus, and was thus a contemporary of Anaximenes. However, the island of Samos was ruled by a tyrant named Polycrates, and to escape an unpleasant regime, Pythagoras moved to Croton, a Greek town in southern Italy (at 39 05N, 17 7 30E), about 530 B.C.
Pythagoras founded what we would nowadays call a cult, a religious group with strict rules about behavior, including diet (no beans), and a belief in the immortality of the soul and reincarnation in different creatures. This of course contrasts with the Milesians' approach to life.
The Pythagoreans believed strongly that numbers, by which they meant the positive integers 1,2,3, and so on, had a fundamental, mystical significance. The numbers were a kind of eternal truth, perceived by the soul, and not subject to the uncertainties of perception by the ordinary senses. In fact, they thought that the numbers had a physical existence, and that the universe was somehow constructed from them. In support of this, they pointed out that different musical notes differing by an octave or a fifth, could be produced by pipes (like a flute), whose lengths were in the ratios of whole numbers, 1:2 and 2:3 respectively. Note that this is an experimental verification of an hypothesis.
They felt that the motion of the heavenly bodies must somehow be a perfect harmony, giving out a music we could not hear since it had been with us since birth. Interestingly, they did not consider the earth to be at rest at the center of the universe. They thought it was round, and orbited about a central point daily, to account for the motion of the stars. Much was wrong with their picture of the universe, but it was not geocentric, for religious reasons. They felt the earth was not noble enough to be the center of everything, where they supposed there was a central fire. (Actually there is some debate about precisely what their picture was, but there is no doubt they saw the earth as round, and accounted for the stars' motion by the earth's rotation.)
To return to their preoccupation with numbers, they coined the term "square" number, for 4,9, etc., drawing square patterns of evenly spaced dots to illustrate this idea. The first square number, 4, they equated with justice. 5 represented marriage, of man (3) and woman (2). 7 was a mystical number. Later Greeks, like Aristotle, made fun of all this.
The Square on the Hypotenuse
Pythagoras is of course most famous for the theorem about right angled triangles, that the sum of the squares of the two sides enclosing the right angle is equal to the square of the long side, called the hypotenuse .

This is easily proved by drawing two diagrams, one having four copies of the triangle arranged so that their hypotenuses form a square, and their right angles are all pointing outward, forming a larger overall square, in the other this larger square is divided differently - the four triangles are formed into two rectangles, set into corners of the square, leaving over two other square areas which are seen to be the squares on the other two sides.
You can prove it yourself--using your fingers--by clicking here!
Actually, it seems very probable that this result was known to the Babylonians a thousand years earlier (see the discussion in the lecture on Babylon), and to the Egyptians, who, for example, used lengths of rope 3, 4 and 5 units long to set up a large right-angle for building and surveying purposes.
Rational and Irrational Numbers
As we discussed above, the Pythagoreans greatly revered the integers, the whole numbers 1, 2, 3,..., and felt that somehow they were the key to the universe. One property of the integers we'll need is the distinction between prime numbers and the rest: prime numbers have no divisors. So, no even number is prime, because all even numbers divide exactly by 2. You can map out the primes by writing down all the integers, say up to 100, cross out all those divisible by 2 (not counting 2 itself), then cross out those divisible by 3, then 5, etc. The numbers surviving this process have no divisors, they are the primes: 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37... . Now, any integer can be written as a product of primes: just divide it systematically first by 2, then if it divides, by 2 again, until you get something that doesn't divide by 2 (and give a whole number). Then redo the process with 3, then 5, until you're done. You can then write, for example, 12 = 2x2x3, 70 = 2x5x7 and so on.
Notice now that if you express a number as a product of its prime factors in this way, then the square of that number is the product of the same factors, but each factor appears twice as often: (70)2 = 2x2x5x5x7x7. And, in particular, note that the square of an even number has 2 appearing at least twice in its list of factors, but the square of an odd number must still be odd: if 2 wasn't on the list of factors of the number, then it won't be on the list for its square, since this is the same list with the factors just appearing twice as often.
Of course, from the earliest times, from Babylon and Egypt, people had been dealing with numbers that were not whole numbers---fractions, for example, or numbers which were integers plus fractions, such as one-and-a-half . This didn't bother the Pythagoreans too much, because after all fractions are simply ratios of two whole numbers, so they fit nicely into a slightly extended scheme.
Let's think about all possible numbers between one and ten, say, including all those with fractional parts, such as 3/2 or 4567/891, to choose a number at random. Suppose we take a piece of paper, mark on it points for the whole numbers 1, 2, 3,...,10. Then we put marks for the halves, then the quarters and three quarters. Next we put marks at the thirds, 4/3, 5/3, 7/3, up to 29/3. Then we do the fifths, then the sevenths,... Then we buy a supercomputer with a great graphics program to put in the higher fractions one after the other at lightning speed!
The question is: is this list of fractions all the numbers there are between one and ten?
In other words, can we prove that there's a number you could never ever reach by this method, no matter how fast your computer?
Two thousand five hundred years ago, the Pythagoreans figured out the answer to this question.
The answer is yes: there are numbers which are not fractions--that is, they cannot be expressed as ratios of integers.
This discovery greatly upset the Pythagoreans, since they revered the integers as the mystical foundation of the universe, and now apparently they were not even sufficient foundation for the numbers. Ironically, this unnerving discovery followed from applying their very own theorem--Pythagoras' theorem--to the simplest possible right-angled triangle: half a square, a triangle with its two shorter sides both equal to one.
This means its long side-the hypotenuse--has a length whose square is two.
We shall now go through their argument showing that the length of this longest side cannot be written as a ratio of two integers, no matter how large you choose the integers to be.
The basic strategy of the proof is to assume it can be written as a ratio of integers, then prove this leads to a contradiction.
So, we assume we can write this number--the length of the longest side--as a ratio of two whole numbers, in other words a fraction m/n . This is the length whose square is 2, so m2/n2 = 2, from which m2 = 2n2.
Now all we have to do is to find two whole numbers such that the square of one is exactly twice the square of the other. How difficult can this be? To get some idea, let's write down the squares of some numbers and look:
12 = 1, 22 = 4, 32 = 9, 42 = 16, 52 = 25, 62 = 36, 72 = 49, 82 = 64, 92 = 81, 102 = 100, 112 = 121, 122 = 144, 132 = 169, 142 = 196, 152 = 225, 162 = 256, 172 = 289, ... .
On perusing this table, you will see we have some near misses: 32 is only one more than twice 22, 72 is only one less than twice 52, and 172 is only one more than twice 122. It's difficult to believe that if we keep at it, we're not going to find a direct hit eventually.
In fact, though, it turns out this never happens, and that's what the Pythagoreans proved. Here's how they did it.
First, assume we canceled any common factors between numerator and denominator.
This means that m and n can't both be even.
Next, notice that the square of an even number is even . This is easy to check: if a is an even number, it can be written a = 2b, where b is another whole number. Therefore, a2 = 2x2xb2, so on fact a2 is not only even, it has 4 as a factor.
On the other hand, the square of an odd number is always odd. If a number doesn't have 2 as a factor, multiplying it by itself won't give a number that has 2 as a factor.
Now, back to the length of the square's diagonal, m/n, with m2 = 2n2.
Evidently, m2 must be even, because it equals 2n2, which has a factor 2.
Therefore, from what we have just said above about squares of even and odd numbers, m must itself be even.
This means, though, that m2 must be divisible by 4.
This means that 2n2 must be divisible by 4, since m2 = 2n2 -- but in this case, n2 must be divisible by 2!
It follows that n must itself be even--BUT we stated at the beginning that we had canceled any common factors between m and n. This would include any factor of 2, so they can't both be even!
Thus a watertight logical argument has led to a contradiction.
The only possible conclusion is: the original assumption is incorrect.
This means that the diagonal length of a square of side 1 cannot be written as the ratio of two integers, no matter how large we are willing to let them be.
This was the first example of an irrational number--one that is not a ratio of integers.
Legend has it that the Pythagoreans who made this discovery public died in a shipwreck.
What's so Important about Irrational Numbers?
The historical significance of the above proof is that it establishes something new in mathematics, which couldn't have been guessed, and, in fact, something the discoverers didn't want to be true. Although fractions very close to the square root of 2 had been found by the Babylonians and Egyptians, there is no hint that they considered the possibility that no fraction would ever be found representing the square root of 2 exactly.
The kind of abstract argument here is far removed from practical considerations where geometry is used for measurement. In fact, it is irrelevant to measurement - one can easily find approximations better than any possible measuring apparatus. The reason the Pythagoreans worked on this problem is because they thought they were investigating the fundamental structure of the universe.
Abstract arguments of this type, and the beautiful geometric arguments the Greeks constructed during this period and slightly later, seemed at the time to be merely mental games, valuable for developing the mind, as Plato emphasized. In fact, these arguments have turned out, rather surprisingly, to be on the right track to modern science, as we shall see.
Change and Constancy in the Physical World
Over the next century or so, 500 B.C.- 400 B.C., the main preoccupation of philosophers in the Greek world was that when we look around us, we see things changing all the time. How is this to be reconciled with the feeling that the universe must have some constant, eternal qualities? Heraclitus, from Ephesus, claimed that "everything flows", and even objects which appeared static had some inner tension or dynamism. Parminedes, an Italian Greek, came to the opposite conclusion, that nothing ever changes, and apparent change is just an illusion, a result of our poor perception of the world.
This may not sound like a very promising debate, but in fact it is, because, as we shall see, trying to analyze what is changing and what isn't in the physical world leads to the ideas of elements, atoms and conservation laws, like the conservation of matter.
The first physicist to give a clear formulation of a possible resolution of the problem of change was Empedocles around 450 B.C., who stated that everything was made up of four elements: earth, water, air and fire. He asserted that the elements themselves were eternal and unchanging. Different substances were made up of the elements in different proportions, just as all colors can be created by mixing three primary colors in appropriate proportions. Forces of attraction and repulsion (referred to as love and strife) between these elements cause coming together and separation, and thus apparent change in substances. Another physicist, Anaxogoras, argued that no natural substance can be more elementary than any other, so there were an infinite number of elements, and everything had a little bit of everything else in it. He was particularly interested in nutrition, and argued that food contained small amounts of hair, teeth, etc., which our bodies are able to extract and use.
The most famous and influential of the fifth century B.C. physicists, though, were the atomists, Leucippus of Miletus and Democritus of Abdera. They claimed that the physical world consisted of atoms in constant motion in a void, rebounding or cohering as they collide with each other. Change of all sorts is thus accounted for on a basic level by the atoms separating and recombining to form different materials. The atoms themselves do not change. This sounds amazingly like our modern picture, but of course it was all conjecture, and when they got down to relating the atoms to physical properties, Democritus suggested, for example, that things made of sharp, pointed atoms tasted acidic, those of large round atoms tasted sweet. There was also some confusion between the idea of physical indivisibility and that of mathematical indivisibility, meaning something that only exists at a point. The atoms of Democritus had shapes, but it is not clear if he realized this implied they could, at least conceptually, be divided. This caused real problems later on, especially since at that time there was no experimental backing for an atomic theory, and it was totally rejected by Aristotle and others.
Hippocrates and his Followers
It is also worth mentioning that at this same time, on the island of Kos (see map) just a few miles from Miletus, lived the first great doctor, Hippocrates. He and his followers adopted the Milesian point of view, applied to disease, that it was not caused by the gods, even epilepsy, which was called the sacred disease, but there was some rational explanation, such as infection, which could perhaps be treated.
Here's a quote from one of Hippocrates' followers, writing about epilepsy in about 400 B.C.:
"It seems to me that the disease called sacred ... has a natural cause, just as other diseases have. Men think it divine merely because they do not understand it. But if they called everything divine that they did not understand, there would be no end of divine things! ... If you watch these fellows treating the disease, you see them use all kinds of incantations and magic--but they are also very careful in regulating diet. Now if food makes the disease better or worse, how can they say it is the gods who do this? ... It does not really matter whether you call such things divine or not. In Nature, all things are alike in this, in that they can be traced to preceding causes."
The Hippocratic doctors criticized the philosophers for being too ready with postulates and hypotheses, and not putting enough effort into careful observation. These doctors insisted on careful, systematic observation in diagnosing disease, and a careful sorting out of what was relevant and what was merely coincidental. Of course, this approach is the right one in all sciences.
Plato
In the fourth century B.C., Greek intellectual life centered increasingly in Athens, where first Plato and then Aristotle established schools, the Academy and the Lyceum respectively, which were really the first universities, and attracted philosophers and scientists from all over Greece.
Actually, this all began somewhat earlier with Socrates, Plato's teacher, who, however, was not a scientist, and so not central to our discussion here. One of Socrates' main concerns was how to get the best people to run the state, and what were the ideal qualities to be looked for in such leaders. He believed in free and open discussion of this and other political questions, and managed to make very clear to everybody that he thought the current leaders of Athens were a poor lot. In fact, he managed to make an enemy of almost everyone in a position of power, and he was eventually brought to trial for corrupting the young with his teachings. He was found guilty, and put to death.
This had a profound effect on his pupil Plato, a Greek aristocrat, who had originally intended to involve himself in politics. Instead, he became an academic-in fact, he invented the term! He, too, pondered the question of what is the ideal society, and his famous book The Republic is his suggested answer. He was disillusioned with Athenian democracy after what had happened to Socrates, and impressed with Sparta, an authoritarian state which won a war, the Peloponnesian war, against Athens. Hence his Republic has rather a right wing, antidemocratic flavor. However, he tries to ensure that the very best people in each generation are running the state, and he considers, being a philosopher, that the best possible training for these future leaders is a strong grounding in logic, ethics and dealing with abstract ideas. This is made particularly clear on p 67,8 of Lloyd, where a quote from the Republic is given, in which Socrates is emphasizing how important it is for future leaders to study astronomy. Glaucon agrees that astronomy is useful in navigation, military matters and accurately determining seasons for planting, etc., to which Socrates responds emphatically that these reasons are not nearly as important as the training in abstract reasoning it provides.
Plato, then, had a rather abstract view of science, reminiscent of the Pythagoreans. In particular, he felt that the world we apprehend with our senses is less important than the underlying world of pure eternal forms we perceive with our reason or intellect, as opposed to our physical senses. This naturally led him to downgrade the importance of careful observation, for instance in astronomy, and to emphasize the analytical, mathematical approach.
Plato believed the universe was created by a rational god, who took chaotic matter and ordered it, but he also believed that because of the inherent properties of the matter itself, his god was not omnipotent, in the sense that there were limits as to how good the universe could be: one of his examples was that smart people have large brains (he thought), but if you make the brain too large by having a very thin skull, they won't last long! He felt this need to compromise was the explanation of the presence of evil in a universe created by a beneficent god.
Plato's concentration on perfect underlying forms did in fact lead to a major contribution to astronomy, despite his own lack of interest in observation. He stated that the main problem in astronomy was to account for the observed rather irregular motion of the planets by some combination of perfect motions, that is, circular motions. This turned out to be a very fruitful way of formulating the problem.
Plato's theory of matter was based on Empedocles' four elements, fire, air, water and earth. However, he did not stop there. He identified each of these elements with a perfect form, one of the regular solids, fire with the tetrahedron, air with the octahedron, water with the icosahedron and earth with the cube. He divided each face of these solids into elementary triangles (45 45 90 and 30 60 90) which he regarded as the basic units of matter. He suggested that water could be decomposed into fire and air by the icosahedron breaking down to two octahedra and a tetrahedron . This looks like a kind of atomic or molecular theory, but his strong conviction that all properties of matter could eventually be deduced by pure thought, without resort to experiment, proved counterproductive to the further development of scientific understanding for centuries. It should perhaps be mentioned, though, that the latest theory in elementary particle physics, string theory, known modestly as the theory of everything, also claims that all physical phenomena should be deducible from a very basic mathematical model having in its formulation no adjustable parameters--a perfect form.
References
Lloyd, G. E. R. (1970). Early Greek Science: Thales to Aristotle, Norton.
Heath, Sir Thomas (1921, 1981). A History of Greek Mathematics, Volume I. Dover.