previous
index
next
Special Relativity: What Time is it?
Michael Fowler, UVa
Special Relativity in a Nutshell
Einstein’s Theory of Special Relativity, discussed in the last
lecture, may be summarized as follows:
The
Laws of Physics are the same in any Inertial Frame of Reference. (Such
frames move at steady velocities with respect to each other.)
These
Laws include in particular Maxwell’s Equations describing electric and
magnetic fields, which predict that light always travels at a particular speed
c, equal to about 3×108 meters per second, that is,186,300
miles per second.
It
follows that any measurement of the speed of any flash of light by any observer
in any inertial frame will give the same answer c.
We have already noted one counter-intuitive consequence of this, that two
different observers moving relative to each other, each measuring the speed of
the same blob of light relative to himself, will both get c,
even if their relative motion is in the same direction as the motion of the
blob of light.
We shall now explore how this simple assumption changes everything we
thought we understood about time and space.
A Simple but Reliable Clock
We mentioned earlier that each of our (inertial) frames of reference is calibrated
(had marks at regular intervals along the walls) to measure distances, and has
a clock to measure time. Let us now get more specific about the
clock—we want one that is easy to understand in any frame of reference. Instead
of a pendulum swinging back and forth, which wouldn’t work away from the
earth’s surface anyway, we have a blip of light bouncing back and forth
between two mirrors facing each other. We call this device a light
clock. To really use it as a timing device we need some way to count
the bounces, so we position a photocell at the upper mirror, so that it catches
the edge of the blip of light. The photocell clicks when the light hits
it, and this regular series of clicks drives the clock hand around, just as for
an ordinary clock. Of course, driving the photocell will eventually use
up the blip of light, so we also need some provision to reinforce the blip
occasionally, such as a strobe light set to flash just as it passes and thus
add to the intensity of the light. Admittedly, this may not be an easy
way to build a clock, but the basic idea is simple.

It’s easy to figure out how frequently our light clock clicks. If
the two mirrors are a distance w apart, the round trip distance for the
blip from the photocell mirror to the other mirror and back is 2w. Since
we know the blip always travels at c, we find the round trip time to be
2w/c, so this is the time between clicks. This isn’t a very
long time for a reasonable sized clock! The crystal in a quartz watch “clicks
“ of the order of 10,000 times a second. That would correspond to
mirrors about nine miles apart, so we need our clock to click about 1,000 times
faster than that to get to a reasonable size. Anyway, let us assume that
such purely technical problems have been solved.
Looking at Somebody Else’s Clock
Let us now consider two observers, Jack and Jill, each equipped with a
calibrated inertial frame of reference, and a light clock. To be specific,
imagine Jack standing on the ground with his light clock next to a straight
railroad line, while Jill and her clock are on a large flatbed railroad wagon
which is moving down the track at a constant speed v. Jack now decides
to check Jill’s light clock against his own. He knows the time for his clock
is 2w/c between clicks. Imagine it to be a slightly misty day, so with
binoculars he can actually see the blip of light bouncing between the mirrors
of Jill’s clock. How long does he think that blip takes to make a round
trip? The one thing he’s sure of is that it must be moving at c =
186,300 miles per second, relative to him—that’s what Einstein
tells him. So to find the round trip time, all he needs is the round trip
distance. This will not be 2w, because the mirrors are on the
flatbed wagon moving down the track, so, relative to Jack on the ground, when
the blip gets back to the top mirror, that mirror has moved down the track some
since the blip left, so the blip actually follows a zigzag path as seen from
the ground.
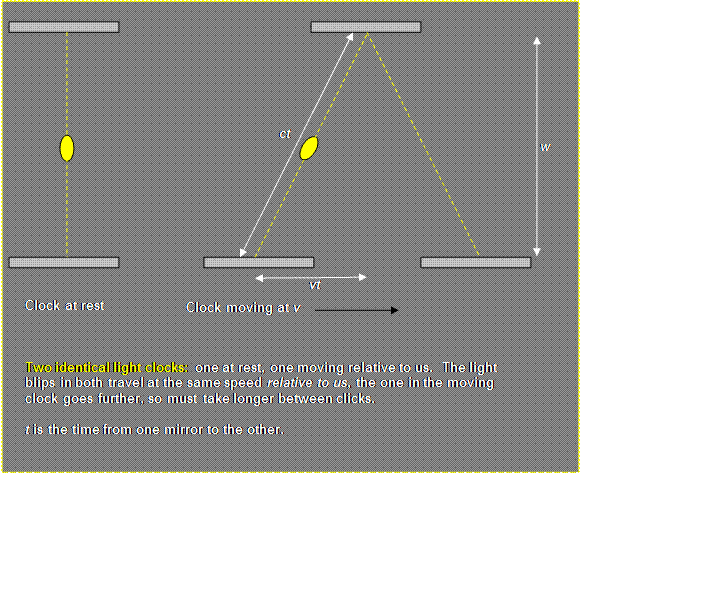
Suppose now the blip in Jill’s clock on the moving flatbed wagon takes
time t to get from the bottom mirror to the top mirror as measured by
Jack standing by the track. Then the length of the “zig” from the
bottom mirror to the top mirror is necessarily ct, since that is the
distance covered by any blip of light in time t. Meanwhile, the
wagon has moved down the track a distance vt, where v is the
speed of the wagon. This should begin to look familiar—it is precisely
the same as the problem of the swimmer who swims at speed c relative to
the water crossing a river flowing at v! We have again a
right-angled triangle with hypotenuse ct, and shorter sides vt
and w.
For an animation, click here!
From Pythagoras, then,
c²t²
= v²t² + w²
so
t²(c²
- v²) = w²
or
t²(1 - v²/c²)
= w²/c²
and, taking the square root of each side, then doubling to get the round
trip time, we conclude that Jack sees the time between clicks for Jill’s
clock to be:

Of course, this gives the right answer 2w/c
for a clock at rest, that is, v = 0.
This means that Jack sees Jill’s light clock to be going slow—a
longer time between clicks—compared to his own identical clock. Obviously,
the effect is not dramatic at real railroad speeds. The correction factor
is 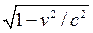 ,
which differs from 1 by about one part in a trillion even for a bullet train! Nevertheless,
the effect is real and can be measured, as we shall discuss later.
,
which differs from 1 by about one part in a trillion even for a bullet train! Nevertheless,
the effect is real and can be measured, as we shall discuss later.
It is important to realize that the only reason we chose a light
clock, as opposed to some other kind of clock, is that its motion is very easy
to analyze from a different frame. Jill could have a collection of clocks
on the wagon, and would synchronize them all. For example, she could hang
her wristwatch right next to the face of the light clock, and observe them
together to be sure they always showed the same time. Remember, in her
frame her light clock clicks every 2w/c seconds, as it is designed to
do. Observing this scene from his position beside the track, Jack will
see the synchronized light clock and wristwatch next to each other, and, of
course, note that the wristwatch is also running slow by the factor 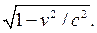 In
fact, all her clocks, including her pulse, are slowed down by this
factor according to Jack. Jill is aging more slowly because she’s
moving!
In
fact, all her clocks, including her pulse, are slowed down by this
factor according to Jack. Jill is aging more slowly because she’s
moving!
But this isn’t the whole story—we must now turn everything
around and look at it from Jill’s point of view. Her inertial
frame of reference is just as good as Jack’s. She sees his
light clock to be moving at speed v (backwards) so from her point of
view his light blip takes the longer zigzag path, which means his
clock runs slower than hers. That is to say, each of them will see
the other to have slower clocks, and be aging more slowly. This
phenomenon is called time dilation. It has been verified in recent
years by flying very accurate clocks around the world on jetliners and finding
they register less time, by the predicted amount, than identical clocks left on
the ground. Time dilation is also very easy to observe in elementary
particle physics, as we shall discuss in the next section.
Fitzgerald Contraction
Consider now the following puzzle: suppose Jill’s clock is equipped
with a device that stamps a notch on the track once a second. How far
apart are the notches? From Jill’s point of view, this is pretty
easy to answer. She sees the track passing under the wagon at v meters
per second, so the notches will of course be v meters apart. But
Jack sees things differently. He sees Jill’s clocks to be running slow,
so he will see the notches to be stamped on the track at intervals of  seconds
(so for a relativistic train going at v = 0.8c, the notches are
stamped at intervals of 5/3 = 1.67 seconds). Since Jack agrees with Jill that
the relative speed of the wagon and the track is v, he will assert the
notches are not v meters apart, but
seconds
(so for a relativistic train going at v = 0.8c, the notches are
stamped at intervals of 5/3 = 1.67 seconds). Since Jack agrees with Jill that
the relative speed of the wagon and the track is v, he will assert the
notches are not v meters apart, but 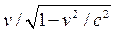 meters apart, a greater
distance. Who is right? It turns out that Jack is right, because
the notches are in his frame of reference, so he can wander over to them with a
tape measure or whatever, and check the distance. This implies that as a
result of her motion, Jill observes the notches to be closer together by a
factor
meters apart, a greater
distance. Who is right? It turns out that Jack is right, because
the notches are in his frame of reference, so he can wander over to them with a
tape measure or whatever, and check the distance. This implies that as a
result of her motion, Jill observes the notches to be closer together by a
factor 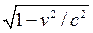 than
they would be at rest. This is called the Fitzgerald contraction,
and applies not just to the notches, but also to the track and to Jack—everything
looks somewhat squashed in the direction of motion!
than
they would be at rest. This is called the Fitzgerald contraction,
and applies not just to the notches, but also to the track and to Jack—everything
looks somewhat squashed in the direction of motion!
Experimental Evidence for Time Dilation: Dying Muons
The first clear example of time dilation was provided over fifty years ago
by an experiment detecting muons. (David H. Frisch and James A.
Smith, Measurement of the Relativistic Time Dilation Using Muons, American
Journal of Physics, 31, 342, 1963). These particles are produced
at the outer edge of our atmosphere by incoming cosmic rays hitting the first
traces of air. They are unstable particles, with a “half-life”
of 1.5 microseconds (1.5 millionths of a second), which means that if at a
given time you have 100 of them, 1.5 microseconds later you will have about 50,
1.5 microseconds after that 25, and so on. Anyway, they are constantly
being produced many miles up, and there is a constant rain of them towards the
surface of the earth, moving at very close to the speed of light. In
1941, a detector placed near the top of Mount Washington (at 6000 feet above
sea level) measured about 570 muons per hour coming in. Now these muons
are raining down from above, but dying as they fall, so if we move the detector
to a lower altitude we expect it to detect fewer muons because a fraction of
those that came down past the 6000 foot level will die before they get to a
lower altitude detector. Approximating their speed by that of light, they
are raining down at 186,300 miles per second, which turns out to be,
conveniently, about 1,000 feet per microsecond. Thus they should reach
the 4500 foot level 1.5 microseconds after passing the 6000 foot level, so, if
half of them die off in 1.5 microseconds, as claimed above, we should only expect
to register about 570/2 = 285 per hour with the same detector at this level. Dropping
another 1500 feet, to the 3000 foot level, we expect about 280/2 = 140 per
hour, at 1500 feet about 70 per hour, and at ground level about 35 per hour. (We
have rounded off some figures a bit, but this is reasonably close to the
expected value.)
To summarize: given the known rate at which these raining-down unstable
muons decay, and given that 570 per hour hit a detector near the top of Mount
Washington, we only expect about 35 per hour to survive down to sea level. In
fact, when the detector was brought down to sea level, it detected about 400
per hour! How did they survive? The reason they didn’t decay
is that in their frame of reference, much less time had passed. Their
actual speed is about 0.994c, corresponding to a time dilation factor of
about 9, so in the 6 microsecond trip from the top of Mount Washington to sea
level, their clocks register only 6/9 = 0.67 microseconds. In this period
of time, only about one-quarter of them decay.
What does this look like from the muon’s point of view? How do
they manage to get so far in so little time? To them, Mount Washington
and the earth’s surface are approaching at 0.994c, or about 1,000 feet
per microsecond. But in the 0.67 microseconds it takes them to get to sea
level, it would seem that to them sea level could only get 670 feet closer, so
how could they travel the whole 6000 feet from the top of Mount Washington? The
answer is the Fitzgerald contraction. To them, Mount Washington is
squashed in a vertical direction (the direction of motion) by a factor of 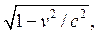 the
same as the time dilation factor, which for the muons is about 9. So, to
the muons, Mount Washington is only 670 feet high—this is why they can
get down it so fast!
the
same as the time dilation factor, which for the muons is about 9. So, to
the muons, Mount Washington is only 670 feet high—this is why they can
get down it so fast!
previous
index
next



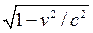 ,
which differs from 1 by about one part in a trillion even for a bullet train! Nevertheless,
the effect is real and can be measured, as we shall discuss later.
,
which differs from 1 by about one part in a trillion even for a bullet train! Nevertheless,
the effect is real and can be measured, as we shall discuss later. 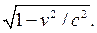 In
fact, all her clocks, including her pulse, are slowed down by this
factor according to Jack. Jill is aging more slowly because she’s
moving!
In
fact, all her clocks, including her pulse, are slowed down by this
factor according to Jack. Jill is aging more slowly because she’s
moving!