previous index next

More Relativity: The Train and The Twins

Michael Fowler, UVa

Einstein’s Definition of Common Sense

As you can see from the lectures so far, although Einstein’s Theory of Special Relativity solves the problem posed by the Michelson-Morley experiment—the nonexistence of an ether—it is at a price. The simple assertion that the speed of a flash of light is always c in any inertial frame leads to consequences that defy common sense. When this was pointed out somewhat forcefully to Einstein, his response was that common sense is the layer of prejudices put down before the age of eighteen. All our intuition about space, time and motion is based on childhood observation of a world in which no objects move at speeds comparable to that of light. Perhaps if we had been raised in a civilization zipping around the universe in spaceships moving at relativistic speeds, Einstein’s assertions about space and time would just seem to be common sense. The real question, from a scientific point of view, is not whether Special Relativity defies common sense, but whether it can be shown to lead to a contradiction. If that is so, common sense wins. Ever since the theory was published, people have been writing papers claiming it does lead to contradictions. The previous lecture, the worked example on time dilation, shows how careful analysis of an apparent contradiction leads to the conclusion that in fact there was no contradiction after all. In this lecture, we shall consider other apparent contradictions and think about how to resolve them. This is the best way to build up an understanding of Relativity.

Trapping a Train in a Tunnel

One of the first paradoxes to be aired was based on the Fitzgerald contraction. Recall that any object moving relative to an observer will be seen by that observer to be contracted, foreshortened in the direction of motion by the ubiquitous factor . Einstein lived in Switzerland, a very mountainous country where the railroads between towns often go through tunnels deep in the mountains.

Suppose a train of length L is moving along a straight track at a relativistic speed and enters a tunnel, also of length L. There are bandits inhabiting the mountain above the tunnel. They observe a short train, one of lengt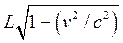h , so they wait until this short train is completely inside the tunnel of length L, then they close doors at the two ends, and the train is trapped fully inside the mountain. Now look at this same scenario from the point of view of someone on the train. He sees a train of length L, approaching a tunnel of length 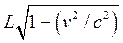, so the tunnel is not as long as the train from his viewpoint! What does he think happens when the bandits close both the doors?

The Tunnel Doors are Closed Simultaneously

The key to understanding what is happening here is that we said the bandits closed the two doors at the ends of the tunnel at the same time. How could they arrange to do that, since the doors are far apart? They could use walkie-talkies, which transmit radio waves, or just flash a light down the tunnel, since it’s long and straight. Remember, though, that the train is itself going at a speed close to that of light, so they have to be quite precise about this timing! The simplest way to imagine them synchronizing the closings of the two doors is to assume they know the train’s timetable, and at a prearranged appropriate time, a light is flashed halfway down the tunnel, and the end doors are closed when the flash of light reaches the ends of the tunnel. Assuming the light was positioned correctly in the middle of the tunnel, that should ensure that the two doors close simultaneously.

Or are They?

Now consider this door-closing operation from the point of view of someone on the train. Assume he’s in an observation car and has incredible eyesight, and there’s a little mist, so he actually sees the light flash, and the two flashes traveling down the tunnels towards the two end doors. Of course, the train is a perfectly good inertial frame, so he sees these two flashes to be traveling in opposite directions, but both at c, relative to the train. Meanwhile, he sees the tunnel itself to be moving rapidly relative to the train. Let us say the train enters the mountain through the “front” door. The observer will see the door at the other end of the tunnel, the “back” door, to be rushing towards him, and rushing to meet the flash of light. Meanwhile, once he’s in the tunnel, the front door is receding rapidly behind him, so the flash of light making its way to that door has to travel further to catch it. So the two flashes of light going down the tunnel in opposite directions do not reach the two doors simultaneously as seen from the train.

The concept of simultaneity, events happening at the same time, is not invariant as we move from one inertial frame to another. The man on the train sees the back door close first, and, if it is not quickly reopened, the front of the train will pile into it before the front door is closed behind the train.

Does the Fitzgerald Contraction Work Sideways?

The above discussion is based on Einstein’s prediction that objects moving at relativistic speed appear shrunken in their direction of motion. How do we know that they’re not shrunken in all three directions, i.e. moving objects maybe keep the same shape, but just get smaller? This can be seen not to be the case through a symmetry argument, also due to Einstein. Suppose two trains traveling at equal and opposite relativistic speeds, one north, one south, pass on parallel tracks. Suppose two passengers of equal height, one on each train, are standing leaning slightly out of open windows so that their noses should very lightly touch as they pass each other. Now, if N (the northbound passenger) sees S as shrunken in height, N’s nose will brush against S’s forehead, say, and N will feel S’s nose brush his chin. Afterwards, then, N will have a bruised chin (plus nose), S a bruised forehead (plus nose). But this is a perfectly symmetric problem, so S would say N had the bruised forehead, etc. They can both get off their trains at the next stations and get together to check out bruises. They must certainly be symmetrical! The only consistent symmetrical solution is given by asserting that neither sees the other to shrink in height (i.e. in the direction perpendicular to their relative motion), so that their noses touch each other. Therefore, the Lorentz contraction only operates in the direction of motion, objects get squashed but not shrunken.

How to Give Twins Very Different Birthdays

Perhaps the most famous of the paradoxes of special relativity, which was still being hotly debated in national journals in the fifties, is the twin paradox. The scenario is as follows. One of two twins—the sister—is an astronaut. (Flouting tradition, we will take fraternal rather than identical twins, so that we can use “he” and “she” to make clear which twin we mean). She sets off in a relativistic spaceship to alpha-centauri, four light-years away, at a speed of, say, 0.6c. When she gets there, she immediately turns around and comes back. As seen by her brother on earth, her clocks ran slowly by the time dilation factor 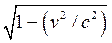, so although the round trip took 8/0.6 years = 160 months by earth time, she has only aged by 4/5 of that, or 128 months. So as she steps down out of the spaceship, she is 32 months younger than her twin brother.

But wait a minute—how does this look from her point of view? She sees the earth to be moving at 0.6c, first away from her then towards her. So she must see her brother’s clock on earth to be running slow! So doesn’t she expect her brother on earth to be the younger one after this trip?

The key to this paradox is that this situation is not as symmetrical as it looks. The two twins have quite different experiences. The one on the spaceship is not in an inertial frame during the initial acceleration and the turnaround and braking periods. (To get an idea of the speeds involved, to get to 0.6c at the acceleration of a falling stone would take over six months.) Our analysis of how a clock in one inertial frame looks as viewed from another doesn’t work during times when one of the frames isn’t inertial—in other words, when one is accelerating.

The Twins Stay in Touch

To try to see just how the difference in ages might develop, let us imagine that the twins stay in touch with each other throughout the trip. Each twin flashes a powerful light once a month, according to their calendars and clocks, so that by counting the flashes, each one can monitor how fast the other one is aging.

The questions we must resolve are:

If the brother, on earth, flashes a light once a month, how frequently, as measured by her clock, does the sister see his light to be flashing as she moves away from earth at speed 0.6c?

How frequently does she see the flashes as she is returning at 0.6c?

How frequently does the brother on earth see the flashes from the spaceship?

Once we have answered these questions, it will be a matter of simple bookkeeping to find how much each twin has aged.

Figuring the Observed Time between Flashes

To figure out how frequently each twin observes the other’s flashes to be, we will use some results from the previous lecture, on time dilation. In some ways, that was a very small scale version of the present problem. Recall that we had two “ground” clocks only one million miles apart. As the astronaut, conveniently moving at 0.6c, passed the first ground clock, both that clock and her own clock read zero. As she passed the second ground clock, her own clock read 8 seconds and the first ground clock, which she photographed at that instant, she observed to read 4 seconds.

That is to say, after 8 seconds had elapsed on her own clock, constant observation of the first ground clock would have revealed it to have registered only 4 seconds. (This effect is compounded of time dilation and the fact that as she moves away, the light from the clock is taking longer and longer to reach her.)

Our twin problem is the same thing, at the same speed, but over a longer time - we conclude that observation of any earth clock from the receding spacecraft will reveal it to be running at half speed, so the brother’s flashes will be seen at the spacecraft to arrive every two months, by spacecraft time.

Symmetrically, as long as the brother on earth observes his sister’s spacecraft to be moving away at 0.6c, he will see light from her flashes to be arriving at the earth every two months by earth time.

To figure the frequency of her brother’s flashes observed as she returns towards earth, we have to go back to our previous example and find how the astronaut traveling at 0.6c observes time to be registered by the second ground clock, the one she’s approaching.

We know that as she passes that clock, it reads 10 seconds and her own clock reads 8 seconds. We must figure out what she would have seen that second ground clock to read had she glanced at it through a telescope as she passed the first ground clock, at which point both her own clock and the first ground clock read zero. But at that instant, the reading she would see on the second ground clock must be the same as would be seen by an observer on the ground, standing by the first ground clock and observing the second ground clock through a telescope. Since the ground observer knows both ground clocks are synchronized, and the first ground clock reads zero, and the second is 6 light seconds distant, it must read -6 seconds if observed at that instant.

Hence the astronaut will observe the second ground clock to progress from -6 seconds to +10 seconds during the period that her own clock goes from 0 to 8 seconds. In other words, she sees the clock she is approaching at 0.6c to be running at double speed.

Finally, back to the twins. During her journey back to earth, the sister will see the brother’s light flashing twice a month. (Evidently, the time dilation effect does not fully compensate for the fact that each succeeding flash has less far to go to reach her.)

We are now ready to do the bookkeeping, first, from the sister’s point of view.

What does she see?

At 0.6c, she sees the distance to alpha-centauri to be contracted by the familiar 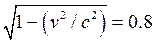to a distance of 3.2 light years, which at 0.6c will take her a time 5.333 years, or, more conveniently, 64 months. During the outward trip, then, she will see 32 flashes from home, she will see her brother to age by 32 months.

Her return trip will also take 64 months, during which time she will see 128 flashes, so over the whole trip she will see 128 + 32 = 160 flashes, so she will have seen her brother to age by 160 months or 13 years 4 months.

What does he see?

As he watches for flashes through his telescope, the stay-at-home brother will see his sister to be aging at half his own rate of aging as long as he sees her to be moving away from him, then aging at twice his rate as he sees her coming back. At first glance, this sounds the same as what she sees—but it isn’t! The important question to ask is when does he see her turn around? To him, her outward journey of 4 light years’ distance at a speed of 0.6c takes her 4/0.6 years, or 80 months. BUT he doesn’t see her turn around until 4 years later, because of the time light takes to get back to earth from alpha-centauri! In other words, he will actually see her aging at half his rate for 80 + 48 = 128 months, during which time he will see 64 flashes.

When he sees his sister turn around, she is already more than half way back! Remember, in his frame the whole trip takes 160 months (8 light years at 0.6c) so he will only see her aging at twice his rate during the last 160 - 128 = 32 months, during which period he will see all 64 flashes she sent out on her return trip.

Therefore, by counting the flashes of light she transmitted once a month, he will conclude she has aged 128 months on the trip, which by his clock and calendar took 160 months. So when she steps off the spacecraft 32 months younger than her twin brother, neither of them will be surprised!

The Doppler Effect

The above analysis hinges on the fact that a traveler approaching a flashing light at 0.6c will see it flashing at double its “natural” rate—the rate observed by someone standing still with the light—and a traveler receding at 0.6c from a flashing light will see it to flash at only half its natural rate.

This is a particular example of the Doppler Effect, first discussed in 1842 by the German physicist Christian Doppler. There is a Doppler Effect for sound waves too. Sound is generated by a vibrating object sending a succession of pressure pulses through the air. These pressure waves are analogous to the flashes of light. If you are approaching a sound source you will encounter the pressure waves more frequently than if you stand still. This means you will hear a higher frequency sound. If the distance between you and the source of sound is increasing, you will hear a lower frequency. This is why the note of a jet plane or a siren goes lower as it passes you. The details of the Doppler Effect for sound are a little different than those for light, because the speed of sound is not the same for all observers—it’s 330 meters per second relative to the air.

An important astronomical application of the Doppler Effect is the red shift. The light from very distant galaxies is redder than the light from similar galaxies nearer to us. This is because the further away a galaxy is, the faster it is moving away from us, as the Universe expands. The light is redder because red light is low frequency light (blue is high) and we see low frequency light for the same reason that the astronaut receding from earth sees flashes less frequently. In fact, the farthest away galaxies we can see are receding faster than the 0.6c of our astronaut!

In the next lecture, we shall brush up on the pre-relativistic concepts of momentum, work and energy to be ready for their relativistic generalizations.

previous index next