Michael Fowler, UVa

Momentum has Direction

As we discussed in the last lecture, even before Newton formulated his laws, Descartes, with a little help from Huygens, had discovered a deep dynamical truth: in any collision, or in fact in any interaction of any kind, the total amount of “momentum”—a measure of motion—always stayed the same. The momentum of a moving object is defined as the product of the mass and the velocity, and so is a vector: it has magnitude and direction.  If you’re standing on frictionless skates and you throw a ball, you move backwards: you have momentum equal in magnitude, but opposite in direction, to that of the ball, so the total momentum (yours plus the ball’s) remains zero.  Rockets work the same way, by throwing material out at high speed.  They do not work by “pushing against the air”, they work by pushing against the stuff they’re pushing out, just as you push against a ball you’re throwing, and it pushes you back, causing your acceleration.

If you still suspect that really rockets push against the air, remember they work just as well in space!  In fact, it was widely believed when Goddard, an early American rocketeer (the Goddard Space Flight Center is named after him) talked about rockets in space, he was wasting his time.  To quote from a New York Times editorial written in 1921: “Professor Goddard does not know the relation between action and reaction and the need to have something better than a vacuum against which to react.  He seems to lack the basic knowledge ladled out daily in our high schools.”  Obviously, the New York Times editorial writers of the time lacked the basic knowledge being ladled out in this course!

In fact, as we discussed, the conservation of momentum in a collision follows from Newton’s laws.  However, it is a more general, simpler, concept—it doesn’t depend at all on details of the interactions, etc. This simplicity evidently appealed to Einstein, who was convinced that when dynamics was reformulated to include the new ideas about time and space, conservation of momentum should still hold true in any inertial frame.  This led him to some surprising conclusions, as we shall see.

Momentum Conservation on the Pool Table

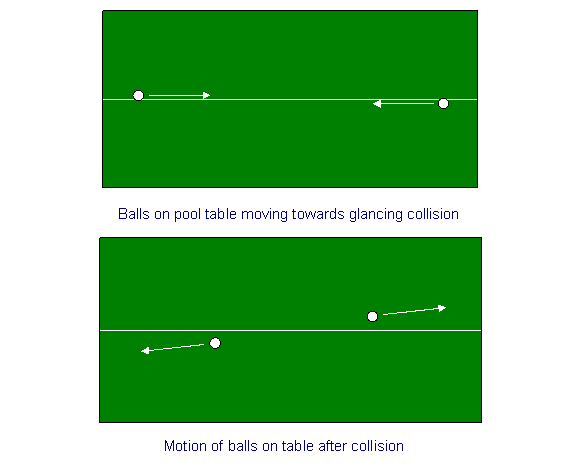
As a warm-up exercise, let us consider conservation of momentum for a collision of two balls on a pool table.  We draw a chalk line down the middle of the pool table, and shoot the balls close to, but on opposite sides of, the chalk line from either end, at the same speed, so they will hit in the middle with a glancing blow, which will turn their velocities through a small angle. In other words, if initially we say their (equal magnitude, opposite direction) velocities were parallel to the x-direction—the chalk line—then after the collision they will also have equal and opposite small velocities in the y-direction. (The x-direction velocities will have decreased very slightly).

A Symmetrical Spaceship Collision

Now let us repeat the exercise on a grand scale.  Suppose somewhere in space, far from any gravitational fields, we set out a string one million miles long.  (It could be between our two clocks in the time dilation experiment).  This string corresponds to the chalk line on the pool table.  Suppose now we have two identical spaceships approaching each other with equal and opposite velocities parallel to the string from the two ends of the string, aimed so that they suffer a slight glancing collision when they meet in the middle.  It is evident from the symmetry of the situation that momentum is conserved in both directions.  In particular, the rate at which one spaceship moves away from the string after the collision—its y-velocity—is equal and opposite to the rate at which the other one moves away from the string.

But now consider this collision as observed by someone in one of the spaceships, call it A.  Before the collision, he sees the string moving very fast by the window, say a few meters away.  After the collision, he sees the string to be moving away, at, say, 15 meters per second.  This is because spaceship A has picked up a velocity perpendicular to the string of 15 meters per second.  Meanwhile, since this is a completely symmetrical situation, an observer on spaceship B would certainly deduce that her spaceship was moving away from the string at 15 meters per second as well.

Just How Symmetrical Is It?

The crucial question is: how fast does an observer in spaceship A see spaceship B to be moving away from the string?  Let us suppose that relative to spaceship A, spaceship B is moving away (in the x-direction) at 0.6c.  First, recall that distances perpendicular to the direction of motion are not Lorentz contracted.  Therefore, when the observer in spaceship B says she has moved 15 meters further away from the string in a one second interval, the observer watching this movement from spaceship A will agree on the 15 meters—but disagree on the one second!  He will say her clocks run slow, so as measured by his clocks 1.25 seconds will have elapsed as she moves 15 meters in the y-direction.

It follows that, as a result of time dilation, this collision as viewed from spaceship A does not cause equal and opposite velocities for the two spaceships in the y-direction.  Initially, both spaceships were moving parallel to the x-axis, there was zero momentum in the y-direction.  So how can we argue there is zero total momentum in the y-direction after the collision, when the identical spaceships do not have equal and opposite velocities?

Einstein Rescues Momentum Conservation

Einstein was so sure that momentum conservation must always hold that he rescued it with a bold hypothesis: the mass of an object must depend on its speed!  In fact, the mass must increase with speed in just such a way as to cancel out the lower y-direction velocity resulting from time dilation.  That is to say, if an object at rest has a mass m, moving at a speed v it will have inertia corresponding to a “relativistic mass” m rel =m/ 1−( v 2 / c 2 ). Then the momentum becomes

                                                 p → = m rel v → =m v → / 1−( v 2 / c 2 ) . 

Note that this relativistic mass increase is an undetectably small effect at ordinary speeds, but as an object approaches the speed of light, the mass increases without limit!

Mass Really Does Increase with Speed

Deciding that masses of objects must depend on speed like this seems a heavy price to pay to rescue conservation of momentum!  However, it is a prediction that is not difficult to check by experiment.  The first confirmation came in 1908, deflecting fast electrons in a vacuum tube.  In fact, the electrons in an old style color TV tube have about half a percent more inertia than electrons at rest, and this must be allowed for in calculating the magnetic fields used to guide them to the screen.

Much more dramatically, in modern particle accelerators very powerful electric fields are used to accelerate electrons, protons and other particles.  It is found in practice that these particles need greater and greater forces for further acceleration as the speed of light is approached.  Consequently, the speed of light is a natural absolute speed limit.  Particles are accelerated to speeds where their relativistic mass is thousands of times greater than their mass measured at rest, usually called the “rest mass”.

…Or Does It?

Actually, there is continuing debate among physicists concerning this concept of relativistic mass.  The debate is largely semantic: no-one doubts that the correct expression for the momentum of a particle having a rest mass m moving with velocity v → is p → = m 1− v 2 / c 2 v → .  But particle physicists especially, many of whom spend their lives measuring particle rest masses to great precision, are not keen on writing this as p → = m rel v → .  They don’t like the idea of a variable mass.  For one thing, it might give the impression that as it speeds up a particle balloons in size, or at least its internal structure somehow alters.  In fact, a relativistic particle just undergoes Lorentz contraction along the direction of motion, like anything else. It goes from a spherical shape towards a disc like shape having the same transverse radius.

 So how can this “mass increase” be understood?  As usual, Einstein had it right: he remarked that every form of energy possesses inertia.  The kinetic energy itself has inertia.  Now “inertia” is a defining property of mass.  The other fundamental property of mass is that it attracts gravitationally. Does this kinetic energy do that?  To see the answer, consider a sphere filled with gas. It will generate a spherically symmetric gravitational field outside itself, of strength proportional to the total mass.  If we now heat up the gas, the gas particles will have this increased (relativistic) mass, corresponding to their increased kinetic energy, and the external gravitational field will have increased proportionally.  (No-one doubts this either.)

  So the “relativistic mass” indeed has the two basic properties of mass: inertia and gravitational attraction.  (As will become clear in the following lectures, this relativistic mass is nothing but the total energy, with the rest mass itself now seen as energy.)

On a more trivial level, some teachers object to introducing relativistic mass because they fear students will assume the kinetic energy of a relativistically moving particle is just 1 2 m v → 2 using the relativistic mass—it isn’t, as we shall see shortly.

Footnote:  For anyone who might go on sometime to a more mathematically sophisticated treatment, it should be added that the rest mass plays an important role as an invariant on going from one frame of reference to another, but the "relativistic mass" used here is really just the first component (the energy) of the four dimensional energy-momentum vector of a particle, and so is not an invariant.

Kinetic Energy and Mass for Very Fast Particles

Let’s think about the kinetic energy of one of these particles traveling close to the speed of light.  Recall that in an earlier lecture we found the kinetic energy of an ordinary non-relativistic (i.e. slow moving) mass m was 1 2 m v 2 . The way we did that was by considering how much work we had to do to raise it through a certain height: we had to exert a force equal to its weight W to lift it through height h, the total work done, or energy expended, being force x distance, Wh.  As it fell back down, the force of gravity, W, did an exactly equal amount of work Wh on the falling object, but this time the work went into accelerating the object, to give it kinetic energy.  Since we know how fast falling objects pick up speed, we were able to conclude that the kinetic energy was 1 2 m v 2 . (For details, see the previous lecture.)

More generally, we could have accelerated the mass with any constant force F, and found the work done by the force (force x distance) to get it to speed v from a standing start.  The kinetic energy of the mass, E= 1 2 m v 2 , is exactly equal to the work done by the force in bringing the mass up to that speed.  (It can be shown in a similar way that if a force is applied to a particle already moving at speed u, say, and it is accelerated to speed v, the work necessary is 1 2 m v 2 − 1 2 m u 2 . )

It is interesting to try to repeat the exercise for a particle moving very close to the speed of light, like the particles in the accelerators mentioned in the previous paragraph.  Newton’s Second Law, in the form

Force = rate of change of momentum

is still true, but close to the speed of light the speed changes negligibly as the force continues to work—instead, the mass increases!  Therefore, we can write to an excellent approximation,

Force = (rate of change of mass) x c 

where as usual c is the speed of light.  To get more specific, suppose we have a constant force F pushing a particle.  At some instant, the particle has mass M, and speed extremely close to c.  One second later, since the force is continuing to work on the particle, and thus increase its momentum from Newton’s Second Law, the particle will have mass M+m say, where m is the increase in mass as a result of the work done by the force.

What is the increase in the kinetic energy E of the particle during that one second period?  By exact analogy with the non-relativistic case reviewed above, it is just the work done by the force during that period.  Now, since the mass of the particle changes by m in one second, m is also the rate of change of mass.  Therefore, from Newton’s Second Law in the form

Force = (rate of change of mass) x c,

we can write

Force =mc.

The increase in kinetic energy E over the one second period is just the work done by the force,

E= force x distance.

Since the particle is moving essentially at the speed of light, the distance the force acts over in the one-second period is just c meters, c=3× 10 8 .  

So the total work the force does in that second is force x distance =mc×c=m c 2 .  

Hence the relationship between the increase in mass of the relativistic particle and its increase in kinetic energy is:

                                                                 E=m c 2 . 

Kinetic Energy and Mass for Slow Particles

Recall that to get Newton’s Laws to be true in all inertial frames, we had to assume an increase of mass with speed by the factor 1/ 1−( v 2 / c 2 ) .  This implies that even a slow-moving object has a tiny increase in mass when it moves!

How does that tiny increase relate to the kinetic energy?  Consider a mass M, moving at speed v,  much less than the speed of light. Its kinetic energy E= 1 2 M v 2 , as discussed above.  Its mass is M/ 1−( v 2 / c 2 ), which we can write as M+m.  What is m? 

Since we’re talking about speeds we are familiar with, like a jet plane, where v/c, is really small, we can use some simple mathematical tricks to make things easier.

The first one is a good approximation for the square root of 1−x when x is a lot less than one:

                                                    1−x ≅1− 1 2 x for x≪1. 

You can easily check this with your calculator: try x= 1 100 , you find 99 100 =0.994987... which is extremely close to 1− 1 2 1 100 =0.995!

The next approximation is

                                                       1 1−x ≅1+x for x≪1. 

This is also easy to check: again take x= 1 100: 1 1−x = 1 99 100 = 100 99 =1.01010…, and 1+x= 101 100 =1.01.

Using these approximations with x=v/c, we can approximate 1−( v 2 / c 2 ) as 1− 1 2 ( v 2 / c 2 ), and then 1/( 1− 1 2 ( v 2 / c 2 ) ) as 1+ 1 2 ( v 2 / c 2 ).  

This means the total mass at speed v 

                                             M 1−( v 2 / c 2 ) ≅M( 1+ 1 2 ( v 2 / c 2 ) ), 

and writing this as M+m, we see the mass increase m equals 1 2 M v 2 / c 2 .   

This means that—again—the mass increase m is related to the kinetic energy E by E=m c 2 . 

In fact, it is not difficult to show, using a little calculus, that over the whole range of speed from zero to as close as you like to the speed of light, a moving particle experiences a mass increase related to its kinetic energy by E=m c 2 .  To understand why this isn’t noticed in everyday life, try an example, such as a jet airplane weighing 100 tons moving at 2,000mph.  100 tons is 100,000 kilograms, 2,000mph is about 1,000 meters per second.  That’s a kinetic energy 1 2 M v 2 of ½×10¹¹joules, but the corresponding mass change of the airplane down by the factor c 2 ,9× 10 16 ,  giving an actual mass increase of about half a milligram, not too easy to detect!

E = mc²

We have seen above that when a force does work accelerating a body to give it kinetic energy, the mass of the body increases by an amount equal to the total work done by the force, the energy E transferred, divided by c 2 . What about when a force does work on a body that is not speeding it up, so there is no increase in kinetic energy?  For example, what if I just lift something at a steady rate, giving it potential energy?  It turns out that in this case, too, there is a mass increase given by E=m c 2 , of course unmeasurably small for everyday objects.

However, this is a measurable and important effect in nuclear physics.  For example, the helium atom has a nucleus which has two protons and two neutrons bound together very tightly by a strong nuclear attraction force.  If sufficient outside force is applied, this can be separated into two “heavy hydrogen” nuclei, each of which has one proton and one neutron.  A lot of outside energy has to be spent to achieve this separation, and it is found that the total mass of the two heavy hydrogen nuclei is measurably (about half a percent) heavier than the original helium nucleus.  This extra mass, multiplied by c 2 , is just equal to the energy needed to split the helium nucleus into two.  Even more important, this energy can be recovered by letting the two heavy hydrogen nuclei collide and join to form a helium nucleus again.  (They are both electrically charged positive, so they repel each other, and must come together fairly fast to overcome this repulsion and get to the closeness where the much stronger nuclear attraction kicks in.)  This is the basic power source of the hydrogen bomb, and of the sun.

It turns out that all forms of energy, kinetic and different kinds of potential energy, have associated mass given by E=m c 2 . For nuclear reactions, the mass change is typically of order one thousandth of the total mass, and readily measurable.  For chemical reactions, the change is of order a billionth of the total mass, and not currently measurable.

previous   index