Newton Clarifies the Concept of Force
Michael Fowler
Initial Confusion...
Actually, it took him years. That may seem surprising now, since we are so used to the force of gravity, and ordinary "push" forces, not to mention electrical forces, and so on. In Newton's time, though, it was still widely believed that if something was moving, there had to be a force acting (the old Aristotelian view) and, if you couldn't see an external force acting, there must be one inside the body. This was perhaps partially a confusion of force and momentum: if a body at rest was struck and it began to move, the idea was that the force that struck it was now in the body. After all, if the body in motion now struck you, you would feel the force! And in fact Newton himself believed this at first. In his first foray into mechanics, in 1665, he wrote an essay "On Violent Motion" in which he accepted the view that bodies are kept in motion by a force inside them. (Never at Rest, by Richard S. Westfall, page 144. These notes are largely based on that book.) A little later, after reading Galileo and Descartes, he espoused the concept of inertia, as stated in his First Law (but essentially discovered by Galileo and stated very clearly by Descartes.) Maybe the difficulty here is notational more than conceptual—if the word "force" is used to describe an impulse, which in modern terminology would be force✕time, then this "force" has the same dimensions as momentum, and such an (impulsive) "force" on a body delivers an equivalent amount of momentum to it. If the body were initially at rest, this momentum could be labeled (confusingly!) as the "force" of the motion, which would be delivered as an impulse if the body hit a wall. If this is the correct interpretation of usage at that time, perhaps the viewpoint wasn't really Aristotelian, just the language. But I'm not an expert on this—the interested reader can find references in Westfall's book.
Once he accepted the concept of inertia, that a body will continue in steady motion if no forces are acting on it, it was natural to restrict the definition of force to that which caused change in motion: "Force is the pressure or crowding of one body upon another" and he concluded that there must be a direct relation between the magnitude of the external impact and the change in motion that occurs. Westfall (page 146) quotes Newton: "So much force as is required to destroy any quantity of motion in a body so much is required to generate it, and so much as is required to generate it so much is also required to destroy it." He also wrote a little later: "Tis known by the light of nature, that equal forces shall effect an equal change in equal bodies."
The major advance here is the concept of force as an external agent acting on a passive body, and causing a proportionate change in the body's motion—in other words, making a clear distinction between force and momentum.
Continuing his investigation of impact, he analyzed a collision between two bodies of unequal mass in the center of gravity frame of reference. He stated that they had "equal motions" in this frame, both before and after the collision. This could only mean mass✕speed, or momentum (equal and opposite, of course)—the Third Law. (He realized and stated that during such a collision, the center of mass itself would move at a steady speed.)
A Third Law Experiment with Pendulums
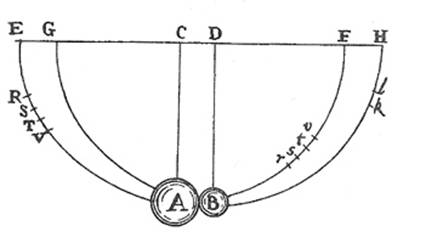
In fact, there is a Third Law experiment in the Principia, in the second Scholium, right after the Laws of Motion and their Corollaries. He collided together two pendulums (about ten feet long) with different masses, to establish that the impacts (i.e. forces) felt by them were equal and opposite, as measured by how far they rebounded.
He went to considerable trouble to account properly for air resistance and imperfect elasticity.
Circular Motion, Starting with Squares
Animation: Applet here!
Next, he addressed the tough problem of circular motion. He
was still thinking of 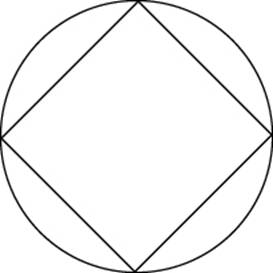 changing motion by a
series of impacts, not a smooth continuous force, but he managed to connect the
two in the following manner. He first
approximated circular motion by square motion—he considered a ball bouncing
abound inside a circle in a square path, making just four impacts per circuit.
The square would have sides of length r x √2, so the time for one circuit would be 4r x √2/v.
changing motion by a
series of impacts, not a smooth continuous force, but he managed to connect the
two in the following manner. He first
approximated circular motion by square motion—he considered a ball bouncing
abound inside a circle in a square path, making just four impacts per circuit.
The square would have sides of length r x √2, so the time for one circuit would be 4r x √2/v.
At each bounce, the velocity towards the center would suddenly change by 2 x v/√2, i.e. one component of the velocity would reverse. Surprisingly, this gives the average acceleration towards the center to be v2/r! (The time for one full circuit is 4r x √2/v, and the total velocity change towards the center generated by the four hits is 4 x 2 x v/√2, giving velocity change/unit time = v2/r.) Of course, this is a bit tricky, since we're not quite treating velocity as a vector, it would be better to take one quarter of a revolution, from the midpoint of one side of the square to the midpoint of the next side. But this is only Newton's first step—he then went on to demonstrate that the same v2/r result followed if the square were replaced by a many-sided equilateral polygon. Finally, taking the limit of a polygon with an infinite number of sides gave a circle, and in this limit it was clear that the acceleration was precisely towards the center. See our Applet.
Defending Copernicus, and Measuring g with a Conical Pendulum
Part of his motivation in doing this was to address a problem discussed earlier by Galileo, namely, if the earth is rotating, why don't we get thrown off? You can only answer this properly if you understand that the acceleration in circular motion is v2/r. This is to be compared with g.
At this point, Newton realized that he could improve on Galileo's value for g with a simple experiment! (Westfall, page 150.) If he could make a measurement on a conical pendulum having an angle of exactly 45⁰, g would equal v2/r. He used a pendulum 81 inches long, and stated that the value of g the experiment gave was such that a body would fall 200 inches in the first second from rest. This is very close to the correct value. He found gravity to be about 300 times stronger than the "centrifugal force", so there is no danger of being thrown off the earth by its rotation!
Having grasped the concept of acceleration in circular motion (which Huyghens found independently) Newton (the famous apple story) connected the circular motion of the moon with the downward acceleration of the apple, and thereby came upon the inverse square law of gravitation, which he demonstrated also accounted for Kepler's Laws.