Experimento de Michelson-Morley
Michael
Fowler, University of Virginia
Translated
by Lydia Alvarez, Universidad Autónoma de Baja California
Applet of the experiment Flashlet
French
Translation of this Lecture
Index
of Lectures and Overview of the Course
La naturaleza de la luz
Como
resultado de los esfuerzos de Michelson, en 1879 se supo que la velocidad de la
luz era de 299,900 kilómetros por segundo con un probable error de
aproximadamente 50 kilómetros por segundo. Esta medición, hecha tomando el
tiempo que un destello de luz tarda en viajar entre espejos en Annapolis,
concordó bien con mediciones menos directas basadas en observaciones
astronómicas. Con todo, esto no clarificó en realidad la naturaleza de la luz. Doscientos años
antes,
La naturaleza ondulatoria
del sonido
En
realidad, el sonido ya era bastante comprendido por los antiguos griegos. El
detalle esencial del que ellos se habían dado cuenta es que el sonido es
generado por un objeto material que vibra, como una campana, una cuerda o la
piel de un tambor. Su explicación era que la piel vibrante, por ejemplo, empuja
y hala alternativamente el aire justo sobre ella, enviando ondas de compresión
y descompresión (conocida como rarefacción), como los círculos de rizos que se
expanden a partir de una perturbación en la superficie de un estanque. Al
llegar al oído, estas ondas empujan y halan el tímpano con la misma frecuencia
(es decir, el mismo número de empujones por segundo) a la que la fuente
original está vibrando, y los nervios transmiten del oído al cerebro tanto la
intensidad (lo ruidoso) como la frecuencia (la nota musical) del sonido.
Existe un par de propiedades especiales de las ondas de sonido (en realidad, de todas las ondas) que vale más que las mencionemos ahora. La primera se llama interferencia. Esto se demuestra más fácilmente con ondas de agua. Si pones dos dedos en una bañera llena de agua, tocando apenas la superficie y separados más o menos treinta centímetros, y los vibras al mismo ritmo para obtener dos circulos de rizos que se expanden, notarás que en donde los rizos se traslapan se forman patrones de ondas complicados. El punto esencial es que en los lugares en que las crestas de las ondas de las dos fuentes llegan al mismo tiempo, las ondas trabajarán juntas y el agua estará muy perturbada, pero en los puntos donde la cresta de una fuente llegue al mismo tiempo que el valle de la otra, las ondas se cancelarán una con otra, y el agua casi no se moverá. Puedes escuchar este efecto para ondas de sonido tocando una nota constante a través de bocinas estéreo. Mientras te mueves dentro de un cuarto, escucharás grandes variaciones en la intensidad del sonido. Por supuesto, las reflexiones de las paredes complican el patrón. Esta gran variación en volumen no es muy notable cuando el estéreo está tocando música, porque la música está hecha de muchas frecuencias, y éstas cambian todo el tiempo. Las diferentes frecuencias, o notas, tienen sus puntos silenciosos en el cuarto en diferentes lugares. El otro punto que debe mencionarse es que el sonido agudo, de alta frecuencia, es mucho más direccional que el sonido grave, de baja frecuencia. En realidad no importa en donde pones la bocina de graves, de cualquier modo el sonido parece estar por todos lados. Por otra parte, es bastante difícil conseguir que una bocina emita las notas altas en todas las direcciones. Si escuchas una bocina barata, las notas altas suenan más fuerte si la bocina apunta hacia tí. Se ha hecho mucho esfuerzo en el diseño de bocinas de agudos, que son pequeñas bocinas especialmente diseñadas para emitir las notas altas sobre un amplio ángulo de direcciones.
¿Es la luz una onda?
Manteniendo
en la mente la minirevisión anterior de las propiedades de las ondas,
reconsideremos la pregunta de si la luz consiste de un flujo de partículas o es
algún tipo de onda. El argumento más fuerte para el modelo de las partículas es
que la luz viaja en línea recta. Puedes escuchar desde el otro lado de la
esquina, al menos hasta cierto punto, pero ciertamente no puedes ver. Además,
para la luz, no existen efectos ondulatorios de interferencia que sean muy
evidentes. Finalmente, se supo por mucho
tiempo, como se ha mencionado, que las ondas de sonido son ondas de presión en
el aire. Si la luz es una onda, ¿que es lo que está oscilando? Es claro que no es simple aire, ya
que la luz llega desde el Sol e incluso desde las estrellas, y sabemos que el
aire no llega hasta allá, o hace mucho tiempo que los planetas habrían reducido
su velocidad debido a la resistencia del aire
A
pesar de todas estas objeciones, alrededor de 1800 se estableció que en
realidad la luz es cierto tipo de onda. La razón de que este hecho haya pasado
desapercibido por tanto tiempo fue que su longitud de onda es en realidad muy corta, aproximadamente
la veinte milésima parte de un centímetro. En contraste, la longitud de onda
más corta del sonido detectable por los humanos tiene una longitud de onda de
aproximadamente un centímetro. El hecho de que la luz viaje en línea recta está
de acuerdo con las observaciones sobre el sonido de que mientras más alta es la
frecuencia (y más corta la longitud de onda) mayor es la tendencia a ir en línea
recta. Del mismo modo, los patrones de interferencia mencionados antes para las
ondas de sonido o los rizos en un estanque varían sobre distancias de más o
menos el mismo tamaño que las longitudes de onda involucradas. Patrones como
esos no serían normalmente visibles ya que estarían en una escala muy
pequeña. En realidad, resulta que sí hay
formas de ver efectos de interferencia con luz. Un efecto familiar son los
múltiples colores que se ven en una burbuja de jabón. Estos aparecen porque al mirar una burbuja de jabón, tú ves
la luz reflejada a ambos lados de una película muy delgada de agua— un grosor
que resulta ser comparable a la longitud de onda de la luz. La luz reflejada de
la capa inferior tiene que viajar un poquito más para alcanzar tu ojo, así que
la onda de luz debe oscilar una o dos veces más antes de llegar a tu ojo en
comparación con la luz reflejada en la capa superior. Lo que ves en realidad es la suma de la luz reflejada en la capa
superior y la reflejada en la capa inferior.
Analizando esto ahora como la suma de dos conjuntos de ondas, la luz
debe ser brillante si las crestas de las dos ondas llegan juntas, pálida si las
crestas de las ondas reflejadas por
la capa superior llegan simultáneamente con los valles reflejados por la capa inferior. Cuál de estas dos
posibilidades ocurre en realidad para la reflexión desde un punto particular en
la película de jabón depende de que tanto más la luz reflejada desde la
superficie inferior tiene que viajar para alcanzar tu ojo en comparación con la
luz de la superficie superior, y eso depende del ángulo de reflexión y el
grosor de la película. Supón ahora que iluminamos la burbuja con luz blanca. La luz blanca está formada por
todos los colores del arco iris, y estos diferentes colores tienen diferentes
longitudes de onda, así que vemos colores reflejados, ya que para una película
en particular, en un ángulo en particular, algunos colores serán reflejados
fuertemente (las crestas llegarán juntas), otros pálidamente, y veremos a
aquellos que predominen.
Si la luz es una onda,
¿qué es lo que está oscilando?
A
pesar de haber establecido que la luz es una onda, aún no hemos contestado una
de las mayores objeciones planteadas anteriormente. ¿Qué es lo que oscila?
Describimos a las ondas de sonido como ondas de presión en el aire. En
realidad, ese es sólo un caso— el sonido viaja también a través de líquidos,
como agua y sólidos, como una barra de acero. Se encuentra experimentalmente
que, si todas las otras condiciones son iguales, el sonido viaja más rápido a
través de un medio que es difícil de comprimir— el material simplemente
recupera su forma más rápido y la onda se mueve a través de él con más rapidez.
Para medios de igual elasticidad, el sonido va más rápido a través del medio
menos denso, esencialmente porque la misma elasticidad puede empujar las cosas
más rápidamente a través de un material más ligero. Entonces, cuando una onda
de sonido pasa, el material— aire, agua o sólido— oscila también. Tomando esto
como una pista, fue natural suponer que la luz debía consistir en ondas en
algún material misterioso, que fue llamado éter,
que rodea y permea todo. Este éter debía también llenar todo el espacio,
llegando hasta las estrellas, ya que podemos verlas, así que el medio debía
estar ahí para transportar la luz. (Nunca podríamos escuchar una explosión en la luna, sin importar su ruido, ya que no
hay aire para transportar el sonido hasta nosotros). Pensemos un poco en qué
propiedades debería tener el éter. Ya que la luz viaja tan rápido, debe ser muy
ligero, y muy difícil de comprimir. Sin embargo, como se mencionó arriba, debe permitir a los
cuerpos sólidos atravesarlo libremente, sin resistencia al éter, o los planetas
estarían reduciendo su velocidad. Así pues podemos imaginarlo como una especie
de viento fantasmal soplando a través de la Tierra. Pero, ¿cómo podemos probar
ésto? ¿Podemos detectarlo?
Detectando el viento de
éter: el experimento de Michelson-Morley
Detectar
el viento de éter fue el siguiente reto que Michelson se puso a sí mismo después
de su triunfo en medir la velocidad de la luz con tanta precisión.
Naturalmente, algo que permite a los cuerpos sólidos atravesarlo libremente es
un poco difícil de atrapar. Pero Michelson se dio cuenta de que, así como la
velocidad del sonido es relativa al aire, la velocidad de la luz debe ser
relativa al éter. Esto debe significar que si pudieras medir la velocidad de la
luz con suficiente precisión, podrías medir la velocidad de la luz que viaja a
favor del viento y compararla con la velocidad de la luz que viaja contra el
viento, y la diferencia de las dos mediciones debería ser el doble de la
velocidad del viento. Desafortunadamente, esto no era tan sencillo. Todas las mediciones precisas
recientes habían usado luz viajando a un espejo distante de ida y de regreso,
así que si hubiera un viento de éter a lo largo de la dirección de los espejos,
tendría efectos opuestos en las dos partes de la medición, dejando un efecto
global muy pequeño. No hay forma técnicamente factible de hacer una determinación
unidireccional de la velocidad de la luz.
En
este punto, Michelson tuvo una idea muy astuta para detectar el viento de éter.
Como él se lo explicó a sus hijos (según su hija), estaba basada en el
siguiente acertijo:
Supongan que tenemos un río de ancho w (digamos, 100 metros), y dos nadadores que nadan a la misma velocidad v en metros por segundo (digamos 5 metros por segundo). El río está fluyendo a una velocidad constante, digamos a 3 metros por segundo. Los nadadores compiten en la siguiente forma: los dos parten del mismo punto en una ribera. Uno nada directamente atravesando el río hasta el punto más cercano en la ribera opuesta, después se da la vuelta y nada de regreso. El otro permanece en un solo lado del río, nadando río arriba una distancia (medida a lo largo de la ribera) exactamente igual al ancho del río, después nada de regreso a su punto de partida. ¿Quién gana?
Consideremos primero el nadador que va río arriba y río abajo. Viajando 100 metros río arriba, la velocidad relativa a la rivera es de sólo 2 metros por segundo, así que le toma 50 segundos. De regreso, la velocidad es de 8 metros por segundo, así que le toma 12.5 segundos, para un tiempo total de 62.5 segundos.
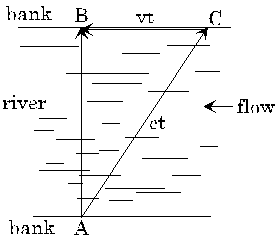
Figura 1 En el tiempo t, el nadador se ha movido ct con respecto al agua, y ha sido
llevado río abajo una distancia vt.
El caso del nadador que atraviesa el flujo es más complicado. No se dirigirá simplemente a la ribera opuesta— el flujo lo halará río abajo. Para tener éxito en alcanzar el punto opuesto de la ribera, el nadador debe en realidad nadar río arriba en el ángulo correcto (por supuesto, un nadador real haría esto automáticamente). Así, el nadador estaría yendo a 5 metros por segundo a un ángulo relativo al río y siendo halado río abajo a una velocidad de 3 metros por segundo. Si el ángulo se escoge correctamente, de modo que el movimiento neto sea perpendicular al río, en un segundo el nadador debe haberse movido cuatro metros en esa dirección—las distancias cubiertas en un segundo forman un triángulo 3, 4, 5. Así, a una velocidad de 4 metros por segundo, el nadador alcanza el otro lado en 25 segundos y regresa en el mismo tiempo, para un tiempo total de 50 segundos. El nadador que atraviesa el río gana. Esto resulta cierto sin importar la velocidad a la que nada. (Por supuesto, ¡la carrera sólo es posible si ellos son capaces de nadar más rápido que la corriente!).
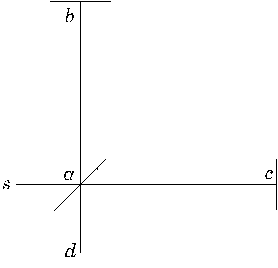
Figura 2 Este diagrama es del artículo original. La fuente de luz está en s, la línea en ángulo de 45 grados es el espejo semi-plateado, b y c son espejos y d es el observador.
La
gran idea de Michelson fue construir una carrera exactamente igual para pulsos
de luz, con el viento de éter jugando el papel del río. El esquema del
experimento es como sigue: un pulso de luz se dirige a un ángulo de 45 grados a
un espejo semi-transparente, semi-plateado, de modo que la mitad del pulso
atraviese el vidrio y la otra mitad sea reflejada. Estos dos semi-pulsos son
los dos nadadores. Los dos se dirigen a espejos distantes que los reflejan de
nuevo al espejo semi-plateado. En este punto, ellos vuelven a ser mitad
reflejados y mitad transmitidos, pero se pone un telescopio detrás del espejo semi-plateado como se
muestra en la figura de modo que la mitad de cada semi-pulso llegará a este
telescopio. Ahora, si sopla un viento de éter, alguien que ve a través del
telescopio verá las mitades de los dos semi-pulsos llegar a tiempos
ligeramente diferentes, ya que uno debe
haber viajado más río arriba y río abajo y el otro más atravesando la corriente.
Para maximizar el efecto, el aparato completo, incluyendo los espejos
distantes, se colocó sobre una gran mesa giratoria, para que pudiera ser
rotado.
Analicemos
qué tanto retraso en el tiempo esperamos encontrar entre la llegada de los dos
semi-pulsos de luz. Tomando la velocidad
de la luz como c metros por segundo
con respecto al éter, y el éter fluyendo a v
metros por segundo a través del laboratorio,
el viajar una distancia w
metros río arriba tomará w/(c-v)
segundos, después, regresar tomará w/(c+v).
El tiempo total del viaje redondo río arriba y río abajo es la suma de estos
dos, que resulta ser 2wc/(c2-v2),
lo que también puede escribirse como (2w/c)×1/(1-v2/c2).
Ahora, podemos suponer con seguridad que la velocidad del éter es mucho menor
que la velocidad de la luz, de otro modo habría sido notado hace mucho tiempo,
por ejemplo, al medir el tiempo de los eclipses de los satélites de Júpiter.
Esto significa que v2/c2
es un número muy pequeño y podemos usar algunos hechos matemáticos útiles para
hacer un poco más fácil el álgebra. Primero, si x es muy pequeño comparado con 1, 1/(1-x) es muy cercano a 1+x.
(Puedes verificarlo con tu calculadora). Otro hecho que necesitaremos en un
minuto es que para x pequeño, la raíz
cuadrada de 1+x es muy cercana a 1+x/2. De cualquier modo, el viaje redondo
río arriba-río abajo puede tomarse con una excelente aproximación como (2w/c)×(1+v2/c2)
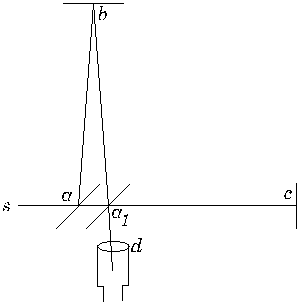
Figura 3 Esta figura también es del artículo original, y muestra la
trayectoria de la luz esperada en relación al éter con un viento de éter
soplando.
Ahora,
¿qué hay con el tiempo del viaje perpendicular al viento? La velocidad real en
esta dirección debe ser visualizada como
en el ejemplo de arriba usando un triángulo rectángulo, con una hipotenusa
igual a la velocidad de la luz c, el
lado más corto la velocidad de flujo del éter v, y el otro lado la velocidad que necesitamos para encontrar el
tiempo recorrido. Del teorema de Pitágoras, entonces, esta velocidad es la raíz
cuadrada de (c2-v2). Ya que esto será igual
en ambos sentidos, el viaje redondo será 2w/raíz(c2-v2). Esto puede escribirse en la forma (2w/c)×1/raíz(1-v2/c2), que aproximaremos como (2w/c)× 1/(1-v2/2c2), usando el comentario de más arriba sobre raíces
cuadradas, y después, reemplazando 1/(1-x)
por 1+x, finalmente anotaremos el
viaje redondo como (2w/c)×(1+v2/2c2).
Mirando
los dos viajes redondos al final de los dos párrafos anteriores, vemos que
difieren por (2w/c)×v2/2c2. Ahora, 2w/c
es justamente el tiempo que la luz tomaría si no hubiera viento de éter en
absoluto, digamos, unas pocas millonésimas de segundo. Si consideramos la velocidad
del viento de éter igual a la velocidad orbital de la Tierra, por ejemplo, v/c
es aproximadamente 1/10,000 así que v2/c2 es aproximadamente
1/100,000,000. Esto significa que el retraso en el tiempo entre los dos pulsos
reflejados por los distintos espejos que alcanzan el microscopio es de
aproximadamente una cienmillonésima de unas pocas millonésimas de segundo.
Parece completamente imposible que un retraso de tiempo tan corto pueda ser
detectado. Sin embargo, esto no
resulta ser el caso, y Michelson fue el primero en imaginar como hacerlo. El
truco es utilizar las propiedades de interferencia
de las ondas de luz. En vez de enviar pulsos de luz, como discutimos arriba,
Michelson lanzó un haz estacionario de luz de un solo color. Esto puede
visualizarse como una secuencia de ondas viajeras, con una longitud de onda de
una veintemilésima de centímetro más o menos. Ahora esta secuencia de ondas se
divide en dos y se refleja como se describió antes. Un conjunto de ondas va con
y contra la corriente y el otro atravesando la corriente. Al final, se reunen
en el telescopio y el ojo. Si aquella a la que le tomó más tiempo está media
longitud de onda detrás, sus valles estarán encima de las crestas de la
primera, se cancelarán y no se verá nada. Si el retraso es menor que eso, aún
habrá algún empalidecimiento. Sin embargo, pequeños errores en la ubicación de
los espejos habrían tenido el mismo efecto. Esta es una razón de porqué el
aparato se construye para ser rotado. Al rotarlo 90 grados, la onda que viaja corriente
arriba y corriente abajo y la que atraviesa la corriente, cambian lugares.
Ahora la otra debería estar detrás. Así, si hubiera un viento de éter, si tú
miras a través del telescopio mientras rotas la mesa giratoria, deberías ver
variaciones en el brillo de la luz que llega.
Para
amplificar la diferencia en tiempos entre las dos trayectorias, en el
experimento real la luz se refleja en ambos sentidos varias veces, como en una
carrera individual por vueltas. Para un diagrama, pulse aquí.
Applet of the experiment Flashlet
Michelson
calculó que una velocidad de viento de éter de sólo dos o tres kilómetros por
segundo tendría efectos observables en este experimento, así que si la
velocidad del viento de éter era comparable con la velocidad de la Tierra en su
órbita alrededor del Sol, sería fácil de ver. En realidad, no se observó nada. La intensidad de la luz no varió
en absoluto. Un tiempo después, el experimento se rediseñó para que un viento
de éter causado por la rotación diaria de la Tierra pudiera detectarse. De
nuevo, no se vio nada. Finalmente,
Michelson se preguntó si el éter estuviera de algún modo pegado a la Tierra,
como el aire en una cabina bajo la cubierta de un barco, así que repitió el
experimento en la cumbre de una alta montaña en California. De nuevo, no
se observó viento de éter. Era
difícil creer que el éter en la inmediata vecindad de la Tierra estuviera
pegado a ella y moviéndose con ella, ya que los rayos de luz de las estrellas
se deflectarían mientras pasan del éter más lejano en movimiento al éter local
fijo.
La
única conclusión posible de esta serie de dificilísimos experimentos era que el
concepto completo de un éter que lo permea todo está equivocado desde el
principio. Michelson fue muy renuente a pensar de este modo. En realidad,
después de 1860, habían surgido nuevas
aportaciones téoricas sobre la naturaleza de la luz, a partir del brillante
trabajo teórico de Maxwell, quien había establecido un conjunto de ecuaciones
que describen como los campos eléctricos y magnéticos pueden originarse uno del
otro. Él había descubierto que estas ecuaciones predecían que podría haber
ondas formadas de campos eléctricos y magnéticos y que la velocidad de estas
ondas, deducida de los experimentos sobre cómo estos campos se enlazan entre
sí, sería de 299,750 kilómetros por segundo. Esta es, obviamente, la velocidad
de la luz, así que es natural suponer que la luz está formada de campos
eléctricos y magnéticos que varían rápidamente. Pero esto conduce a un gran
problema: las ecuaciones de Maxwell predicen una velocidad definida para la
luz, y esta es la velocidad que se
encuentra en las mediciones. Pero, ¿en relación con qué se mide esta
velocidad? La idea de introducir el éter
era dar una representación de la luz que se pareciera a la ya entendida del
sonido, ondas de presión en un medio. La velocidad del sonido en el aire se
mide en relación con el aire. Si el viento sopla hacia tí desde la fuente de
sonido, oirás el sonido más pronto. Si no hay un éter, sin embargo, esta
analogía no es atractiva. Así que, ¿en relación con qué viaja la luz a 299,750
kilómetros por segundo?
Hay otra posibilidad obvia, que se llama la teoría del emisor— la luz viaja a 299,750 kilómetros por segundo con respecto a la fuente de la luz. La analogía aquí es entre la luz emitida por una fuente y balas emitidas por una ametralladora. Las balas salen a una velocidad definida (llamada la velocidad de fuego), relativa al cañon del arma. Si el arma está montada en el frente de un tanque, que se está moviendo hacia delante, entonces en relación con el suelo las balas se están moviendo más rápido que si hubieran sido disparadas desde un tanque en reposo. Entonces, la forma más sencilla de probar la teoría del emisor para la luz, es medir la velocidad de la luz emitida hacia adelante por una linterna que se mueve hacia adelante y ver si excede la velocidad conocida de la luz por una cantidad igual a la velocidad de la linterna. En realidad, este tipo de prueba directa de la teoría del emisor sólo llegó a ser experimentalmente factible después de 1960. Ahora es posible producir partículas, llamadas piones neutros, que decaen cada uno en una pequeña explosión, emitiendo un destello de luz. También es posible hacer que estos piones se muevan hacia delante a 297,000 kilómetros por segundo cuando se autodestruyen, atrapar la luz emitida en la dirección de su movimiento, y medir su velocidad. Se encontró que, a pesar del empuje esperado al haber sido emitidas por una fuente muy rápida, la luz de las pequeñas explosiones viaja en la dirección del movimiento a la velocidad usual de 299, 750 kilómetros por segundo. En el siglo pasado, la teoría del emisor se rechazó ya que se pensó que la aparición de ciertos fenómenos astronómicos, como estrellas dobles, donde dos estrellas rotan una alrededor de la otra, serían afectados. Esos argumentos han sido desde entonces criticados, pero la prueba del pión no tiene ambigüedad. El experimento definitivo fue llevado a cabo por Alvager et al., Physics Letters 12, 260 (1964).
La respuesta de Einstein
Los
resultados de los distintos experimentos discutidos anteriormente parecen
dejarnos realmente anonadados. Evidentemente la luz no es como el sonido, con
una velocidad definida relativa a algún medio subyacente. Sin embargo, no es
tampoco como las balas, con una velocidad definida relativa a la fuente de luz.
Con todo, cuando medimos su velocidad obtenemos siempre el mismo resultado.
¿Cómo pueden todos estos hechos interpretarse de una forma consistente?
Mostraremos como Einstein respondió a esta pregunta en la siguiente clase.
Indice de clase y visión general del curso
Para
detalles técnicos prácticos o arreglos del interferómetro de Michelson, muy
relacionados con la tecnología del experimento de Michelson-Morley, vea la
página de Jacques
Charrier en Nantes, Francia.