More Kepler
Michael Fowler, UVa Physics
Martian Problems
Once Kepler had secured Tycho's data, he set himself the task of once and for all determining the exact orbit of Mars. A preliminary analysis showed the orbit to be very close to a circle, but the sun was not at the center of the circle---it was at a point almost one-tenth of a radius away! Furthermore, it was clear that Mars varied in speed as it went around this orbit, moving fastest when it was closest to the sun (at perihelion) and slowest when it was furthest from the sun (aphelion). Everybody (including Kepler) believed that the motion of planets must be a simple steady motion, or at least made up of simple steady motions, if only it were looked at in the right way. How could the motion of Mars described above be seen as some kind of steady motion?
Actually, a possible solution to this problem had been given long before, by Ptolemy. The method was to introduce another point, called the equant, on the line through the sun and the center of the circular orbit, the equant being on the opposite side of the center from the sun.
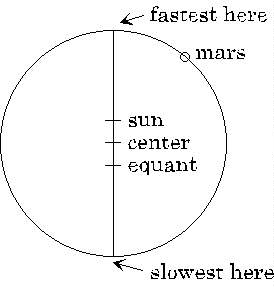
The idea is to try to position this point so that the planet moves around the equant at a steady angular speed. (It is clear from observation that it doesn't move about the center of the circle, or about the sun, at constant angular speed.) This steady motion about the equant is somewhat plausible, because the planet is observed to be moving most slowly when it is furthest from the sun, which is when it is closest to the equant, and vice versa, so if you imagine a spoke going out from the equant point to the planet and sweeping around with the planet, maybe this spoke could be turning at a steady rate.
Ptolemy had shown that observations of the movement of Mars in its orbit were in fact well accounted for by a model of this sort, with the equant point the same distance from the center as the sun, but on the other side, as in the figure above. Kepler, however, had far more accurate records of the movement of Mars, and he was interested in seeing if the model still held up under this closer scrutinizing. He found it didn't. Even adjusting independently the radius of the orbit, the distance of the sun from the center, and the distance of the equant from the center, he found the best possible orbit of this type was still in error by eight minutes of arc (8/60 of a degree) in accounting for the observations. Such an error could not have been detected before Tycho's work. Kepler knew that Tycho's work was accurate to about one minute, and hence the model had to be thrown out. (We might just mention that the reason for taking the equant the same distance from the center as the sun is that this gives the observed ratio of the fastest to the slowest speed, as we shall be discussing later.)
Having thrown out the equant model, though, it was difficult to see what to do next. The natural thought for an astronomer at that time would have been to add an epicycle, that is, to imagine Mars to be going in a small circular orbit about a point which itself goes along the orbit shown above. But Kepler didn't like that approach. The whole business with cycles and epicycles was purely descriptive -- trying to account for the observed planetary motions with a suitable combination of circular motions. Kepler, in contrast, was trying to think dynamically, that is, to understand the planetary motions somehow in terms of a force emanating from the sun sweeping them around in their orbits. Thinking in those terms, adding an epicycle looks unattractive -- what force could be pushing the planet around the small circle, which has nothing at its center?
Pinning Down the Earth's Orbit by Fixing Mars
Kepler realized that to get the kind of precision he needed in analyzing the orbit of Mars, he first needed to have a very accurate picture of the earth's orbit, since all measurements of Mars' position were, obviously, conducted from the earth, so to pin down Mars' position relative to the sun it was necessary to know the earth's position relative to the sun to the required precision. But how could he pin down the earth's position in space accurately? This is rather like being in a boat some distance from shore. If you can see only one landmark, such as a lighthouse, and you have both a compass and a map, that is not enough to really fix your position, because you cannot tell very accurately just how far away the lighthouse is. On the other hand, if you can see two landmarks, in different directions, and measure with your compass the exact directions they lie in from your boat, that is enough to fix your position exactly without any guessing about distances. You just take out your map, draw lines through the two landmarks on the map in the direction your boat lies in from each of them in turn, and the point where the two lines intersect on the map is your location. Essentially, this is just Thales' method as discussed in our review of Greek geometry---the two landmarks form the baseline of a triangle, and we know the direction of the boat from the two ends of the baseline, so we can construct a triangle on this baseline with the boat at the other vertex. Of course, just knowing the angle between the two lines isn't enough---we have to know their individual directions relative to the baseline, which is what we can find with the map and the compass.
The idea is to use this same technique repeatedly to find the location of the earth, and thereby to map out its orbit. The catch is, we need two fixed lighthouses to form the baseline, and we only have one, the sun. The fixed stars won't do, they are infinitely far away for all practical purposes, and just play the role of the compass, giving a fixed direction. Kepler solved the problem of the second fixed lighthouse by a very clever trick. He used Mars. Of course, Mars is moving all the time, and the orbit of Mars is what we are trying to find, so this doesn't seem a promising approach. But one thing we do know is that if Mars is in a certain location at a certain time, it will be in exactly that same place 687.1 days later. Kepler was able to use Tycho's mountains of data to find the exact direction of Mars from the earth at a whole series of times at 687.1 day intervals. By finding the direction of Mars and that of the sun at those times, he had a steady Mars--sun baseline to use in constructing the earth's orbit.
Einstein, in his introduction to Carola Baumgardt's Life of Kepler (ref. 2 below) calls Kepler's use of a "fixed" Mars as described above "an idea of true genius".
In contrast to the orbit of Mars, Kepler found the earth's orbit to be essentially a perfect circle. (It is actually off by about one part in 10,000.) However, the center of the circle is about 1.5 million miles away from the sun, and the speed of the earth in its orbit varies, being greatest at the closest approach to the sun. At the furthest point, the earth is 94.5 million miles from the sun, and it is moving around its orbit at a speed of 18.2 miles per second. At the point of closest approach to the sun, the earth is 91.4 million miles from the sun, and moving around at a speed of 18.8 miles per second. Kepler noticed that there was an interesting relationship among these numbers. The ratio of the speeds, 18.8/18.2 = 1.03, is the inverse of the ratio of the corresponding distances, 91.4/94.5 = 1/1.03.
(NOTE: Kepler didn't know the correct distances we have put in above -- but he did know the ratios of the distances accurately. From observation, it was possible to find ratios of distances, hence the deviation of the orbit from a circle, and also the relative sizes of the orbits of the different planets. However, it was not possible to find the overall size of the system. As we discussed in our review of Greek astronomy, the Greeks estimated the distance from the earth to the sun by careful observation of the sun and the moon when the moon was exactly half full, and clever use of geometry. However, their observational skill wasn't as good as their geometry, and Hipparchus (second century BC) estimated the distance to be about ten million miles. More precise estimates came with the advent of the telescope, and in the 1670's the distance to Mars was measured (see reference 4 below, page 30, for a few more details). This was done by observing it from two points on earth at the same time, carefully noting the precise angle between it and some star nearby in the sky. This made it possible to measure the very small angle between the observations, and therefore to draw a long thin triangle with Mars at the far point, and the small baseline of the triangle being the line between the two telescopes on earth, a known distance. So knowing the small angle between the two long sides makes it possible to find the distance of Mars from earth. Once one distance in the solar system has been determined in this way, all the others can be found, because pure observation is sufficient to find the relative sizes of the orbits.)
Kepler's interpretation of the ratio of the earth's speed in orbit at the nearest and furthest points from the sun being the inverse of the ratios of the distances was that the force he believed to be emanating from the sun, pushing the planets around, was weaker at the greater distance, and so the earth was being pushed around its orbit more slowly. He was not very happy that the force seemed to be just inversely proportional to the distance from the sun, he had expected it would go down as the square of the inverse, since he visualized it as radiating outward rather like the light from the sun, and the intensity of sunlight decreases as the inverse square of the distance on going away from the sun. (The way to see this is to think of the sunlight pouring through an imaginary sphere centered at the sun. Another larger such sphere, having twice the radius of the first, would have four times the area, but the same total amount of sunlight would be shining through it, so the brightness of the light, the intensity per square mile of the sphere, would be down by a factor of four on going from the smaller sphere to the sphere having twice the radius.) Still, the result was undeniable, and evidently his idea about the mechanism needed further work.
The Orbiting Earth "Sweeps Out Area" at a Constant Rate
Actually, the above relationship between speeds and distances at the extreme points of the orbit can be interpreted in an interesting geometrical way that proved important later in understanding the true dynamics of planetary motion. Think of Kepler's spoke, a rod from the center of the sun passing through the center of the earth. As the earth moves around its orbit, this spoke is sweeping out area. What is the rate at which it is sweeping out area? This is not difficult to figure out when the earth is at its closest to the sun. At this point, its motion in orbit is exactly perpendicular to the spoke. The spoke has length 91.4 million miles. In one second, the earth moves 18.8 miles.
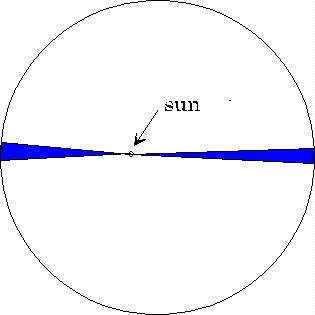
Hence, the area swept out by the spoke in that one second is a long thin triangle, of height 91.4 million miles, and base 18.8 miles. This long thin triangle has an area of 1/2 base x height, or 1/2 x 18.8 x 91.4 million square miles. That is, the earth in its orbital motion, at the closest point in the orbit to the sun, is sweeping out 859 million square miles per second. The important point is that when the earth is furthest from the sun, it is sweeping out area at this same rate, because although the base of the triangular area swept out in one second has shrunk to 18.2 miles, down by a factor of 1/1.03, the height of the triangle has increased by an exactly compensating factor. What Kepler discovered, on analyzing the entire orbit, was that the earth sweeps out area at a constant rate throughout the orbit. This is known as Kepler's Second Law---it is a true uniformity of the motion and an important discovery. This was the "steady motion" he had been looking for. Together with the fact that the earth's orbit was circular to a very high degree of accuracy, this gave a sufficiently precise account of the earth's position in space as a function of time to be able to go on to the main business, the plotting of the more interesting Martian orbit.
Back to Mars
Kepler knew the orbit of Mars was not a circle, in fact he had plotted it and found it to be an oval shape (as he called it) that could be fitted inside a circle as shown here, and deviated from the circle by at most 0.00429 of the oval's half-breadth MC, about one-half of one percent. (Our diagram exaggerates this difference for clarity.)
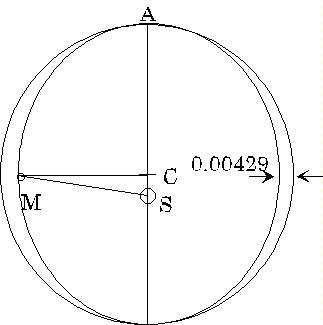
We mean by this that the ratio AC/MC=1.00429. Kepler's figure was constructed directly from Tycho's data. He also measured the angle CMS Mars subtended on the baseline consisting of the sun and the center of the orbit. when the planet was in the position shown. The value of this angle was 50 18' (5 degrees 18 minutes). He stumbled entirely by chance (to quote his own words) on the fact that the secant (one over the cosine) of this angle, the ratio of lengths SM/CM, was 1.00429, and, he says that on finding this number "I felt as if I had been awakened from a sleep".
(This quote from Kepler's book Astronomia Nova, given on page 337 of The Sleepwalkers, is probably the reason Koestler called his book The Sleepwalkers.)
He felt that this could not just be coincidence---there must be a similar relationship between the angle SMC and the distance from the sun at all points on the orbit. He found from the data that this was so, but was still unable to figure out what the curve must be. (Actually, this can be done using Cartesian coordinates, but Descartes didn't invent them until a few years later.) Still, he had stared at his plot long enough to begin to believe that the curve had to be an ellipse, with the sun at one focus, and he then constructed an ellipse by a different approach. At this point it dawned on him that his original analysis also led to an ellipse.
In fact, with hindsight, it is not difficult to show how the numerical coincidence above follows for an ellipse. Kepler found AC/MC=1.00429=MS/MC. This means AC=MS. Taking the sun to be at one focus of the ellipse, label the other focus S'. Constructing the ellipse in the usual way with a piece of string having ends fixed at S, S', we see SM is half the length of the string. But since A is also on the ellipse, the string length is SA+S'A, with S' the other side of C and the same distance from C that S is. Thus the total string length is SA+S'A=2AC, and we see that indeed AC=MS.
The analysis of the Martian orbit we have summarized above, with many wrong turnings and dead ends, took six years and thousands of pages of calculations. It led to two simple laws.
Kepler's Laws
I The planets move in elliptical orbits with the sun at a focus.
II In their orbits around the sun, the planets sweep out equal areas in equal times.
There is also a third Law, which Kepler found by analyzing the orbits of all the known planets:
III The squares of the times to complete one orbit are proportional to the cubes of the average distances from the sun.
To see these Laws in action, click here!
Kepler was probably a bit disappointed when he found this third law. It did not fit in very well with his theory that the planets were driven somehow by spoke-like forces radiating out from the sun. Recall that for a single planet like Mars at varying distances from the sun during its year, the ratio of the fastest speed over the slowest speed in orbit was the inverse of the corresponding distances from the sun, as discussed above, and this suggested that the force emanating from the sun decreased in power as one over the distance away from the sun. Suppose now, as Kepler did, that this same force is driving all the planets. Let us simplify for the moment and take all the orbits to be circular. Let us consider the specific example of the orbits of Jupiter and Saturn, and let us simplify further by supposing Saturn to be just twice as far from the sun as Jupiter is, which is approximately true. This would imply, in Kepler's picture, that Saturn's speed in orbit would be just half of Jupiter's, if it followed the same law as a single planet at different distances. Saturn's orbit would also be twice as far around as Jupiter's, since the distance around a circle is proportional to the radius, so Saturn would be going around an orbit twice as long moving at half the speed, it would take four times as long as Jupiter to complete one orbit. In other words, if the time for one orbit is T, the radius of the orbit R, we would expect T to be proportional to R2, or T2 proportional to R4. However, this is not what is observed---it is found that T2 is proportional to R3.
This suggests that the whole idea of the planets being driven through the ether by invisible spokes attached to the sun, with power diminishing in some way with distance, cannot be made into a consistent theory.
Why Ellipses?
Yet another problem with the picture of planets being driven in orbit around the sun by some kind of system of rotating spokes is that one would expect that to give circular orbits, not ellipses. Earlier astronomers would have just thrown in another epicycle, but Kepler insisted that one should be able to account for the observed motion in terms of driving forces. What kind of added driving force could distort a circular orbit into an ellipse? He realized this could happen if there was an extra force between the earth and the sun that was attractive over half of the orbit, drawing the earth towards the sun, then repulsive over the other half, pushing it away. A known force that could be attractive or repulsive was the magnetic force, and the earth was a magnet---that was why the compass worked! It had been known for a long time that the earth's north pole and south pole were like the two ends of a bar magnet, so an outside magnet that attracted one of them would repel the other. Furthermore, in its path around the sun, the earth always points in the same direction, towards the north star, so for part of the year (our summer) the north pole is closer to the sun, for the other half the south pole is closer. If, then, the sun had a single magnetic pole, it would either attract or repel the earth magnetically depending on which of the earth's magnetic poles was closer at that time of year. This very ingenious theory is another example of Kepler's incredibly inventive mind. It isn't correct---the sun has two magnetic poles, like every other magnet, and in any case the magnetic forces are far too small to affect the orbit measurably.
Kepler on Gravity
Kepler stated flatly that the traditional Aristotelian doctrine that heavy things strive toward the center of the world was completely erroneous. He stated that gravity was a mutual tendency between material bodies toward contact, so the earth draws a stone much more than the stone draws the earth. Heavy bodies are attracted by the earth not because it is the center of the universe, but simply because it contains a lot of material, all of which attracts the heavy body.
To prove he really understood, he wrote: "If two stones were placed anywhere in space near to each other, and outside the reach of force of (other bodies), then they would come together...at an intermediate point, each approaching the other in proportion to the other's mass."
This is actually a completely accurate statement about gravity. Kepler realized that gravity was the key to understanding the tides---that the tides were caused by the waters of the oceans being attracted by the moon's gravitational pull. He wrote: "If the earth ceased to attract the waters of the sea, the seas would rise and flow into the moon..." and went on to add: "If the attractive force of the moon reaches down to the earth, it follows that the attractive force of the earth, all the more, extends to the moon and even farther..."
The above quotes are all from Kepler's introduction to Astronomia Nova, and can be found on pages 342 and 343 of The Sleepwalkers. It seems almost incredible, at least with hindsight, that Kepler could have understood the gravitational force so well, and yet it did not apparently occur to him that it might play a central role in determining the orbital motions of the planets! The essential reason he failed to make the connection was that he believed the planets needed a constant pushing force, in the direction of motion, to keep them going in their orbits. This was the ancient belief that Galileo showed to be false in his discussions of projectiles in Two New Sciences (1638), but that was published well after Astronomia Nova (1609). Galileo's insight about projectiles was extended to the planets by Isaac Newton, and at that point the scientific revolution began in earnest, as we shall see shortly.
References
1. Arthur Koestler, The Sleepwalkers, Arkana Books, London, 1989. I have used this book for many of the facts presented here. It contains references to primary sources, including Kepler's own extensive writings on his life as well as on science.
2. Carola Baumgardt, Johannes Kepler: Life and Letters, Gollancz, London 1952.
3. Eric Rogers, Physics for the Inquiring Mind, Princeton.
4. Michael J. Crowe, Modern Theories of the Universe from Herschel to Hubble, Dover, New York 1994.