Kinetic Theory of Gases

Michael Fowler Physics 142E (from my Physics 152) 4/11/09

Bernoulli's Picture

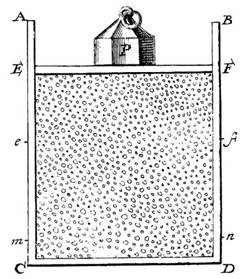BGDaniel Bernoulli, in 1738, was the first to understand air pressure from a molecular point of view. He drew a picture of a vertical cylinder, closed at the bottom, with a piston at the top, the piston having a weight on it, both piston and weight being supported by the air pressure inside the cylinder. He described what went on inside the cylinder as follows: “let the cavity contain very minute corpuscles, which are driven hither and thither with a very rapid motion; so that these corpuscles, when they strike against the piston and sustain it by their repeated impacts, form an elastic fluid which will expand of itself if the weight is removed or diminished…”

(An applet is available here.)  Sad to report, his insight, although essentially correct, was not widely accepted. Most scientists believed that the molecules in a gas stayed more or less in place, repelling each other from a distance, held somehow in the ether .

 

 

 

The Link between Molecular Energy and Pressure

It is not difficult to extend Bernoulli’s picture to a quantitative description, relating the gas pressure to the molecular velocities. As a warm up exercise, let us consider a single perfectly elastic particle, of mass m, bouncing rapidly back and forth at speed v inside a narrow cylinder of length L with a piston at one end, so all motion is along the same line. (For the movie, click here!) What is the force on the piston?

Obviously, the piston doesn’t feel a smooth continuous force, but a series of equally spaced impacts. However, if the piston is much heavier than the particle, this will have the same effect as a smooth force over times long compared with the interval between impacts. So what is the value of the equivalent smooth force?

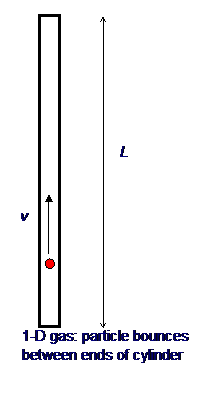Using Newton’s law in the form force = rate of change of momentum, we see that the particle’s momentum changes by 2mv each time it hits the piston. The time between hits is 2L/v, so the frequency of hits is v/2L per second. This means that if there were no balancing force, by conservation of momentum the particle would cause the momentum of the piston to change by 2mv´v/2L units in each second. This is the rate of change of momentum, and so must be equal to the balancing force, which is therefore F = mv2/L.

We now generalize to the case of many particles bouncing around inside a rectangular box, of length L in the x-direction (which is along an edge of the box). The total force on the side of area A perpendicular to the x-direction is just a sum of single particle terms, the relevant velocity being the component of the velocity in the x-direction. The pressure is just the force per unit area, P = F/A. Of course, we don’t know what the velocities of the particles are in an actual gas, but it turns out that we don’t need the details. If we sum N contributions, one from each particle in the box, each contribution proportional to vx2 for that particle, the sum just gives us N times the average value of vx2. That is to say,

where there are N particles in a box of volume V.  Next we note that the particles are equally likely to be moving in any direction, so the average value of vx2 must be the same as that of vy2 or vz2, and since v2 = vx2 + vy2 + vz2, it follows that

This is a surprisingly simple result!  The macroscopic pressure of a gas relates directly to the average kinetic energy per molecule.  Of course, in the above we have not thought about possible complications caused by interactions between particles, but in fact for gases like air at room temperature these interactions are very small.  Furthermore, it is well established experimentally that most gases satisfy the Gas Law over a wide temperature range:

PV = nRT

for n moles of gas, that is, n = N/NA, with NA Avogadro’s number (NA = 6.02×1023 molecules per gram mole)and R the gas constant, R = 8.3 J/mol.K).

Let’s go back to the contribution of one molecule:  introducing Boltzmann’s constant k = R/NA, it is easy to check from our result for the pressure and the ideal gas law that the average molecular kinetic energy is proportional to the absolute temperature,

Boltzmann’s constant k = 1.38.10-23 joules/K.

Finding the Average Molecular Speed Without Knowing the Atomic Mass

Just how fast are these molecules moving on average at room temperature?  Take another look at

Now Nm is the total mass of gas, and Nm/V  = ρ  is therefore the density (1.29 at 0°C, close to 1.2 at 20°C):  so , and putting P = 105 N/m2  and  ρ = 1.2 kg/m3 gives ,  v about  500 meters per second.  (This does averages nitrogen and oxygen:  they don’t differ much, their mean square velocities are inversely proportional to their masses, ratio 14/16.) 

Note:  we didn’t need to know the mass or size of the molecules!  This average speed was figured out long before Avogadro’s number was known!  Maxwell came up with this distribution without knowing the size of molecules.

Notice also that hydrogen molecules with a density roughly 0.083 kg/m3, will have an average speed of order 1900 m/sec. 

The Speed Distribution

Maxwell proved that for a large number N of molecules, the likely number of molecules having speed between v and v+ dv  was

.

Here’s a graph: the blue curve is for room temperature, the red one for T/2 (in kelvins). 

(Note:  in these graphs, the most probably speed is of course at the peak of the curve—the root mean square velocity, however, is higher, because higher speeds contribute disproportionately to the root mean square.  You can easily convince yourself of this by finding the average, then the root mean square, of two numbers, like 1 and 2.)

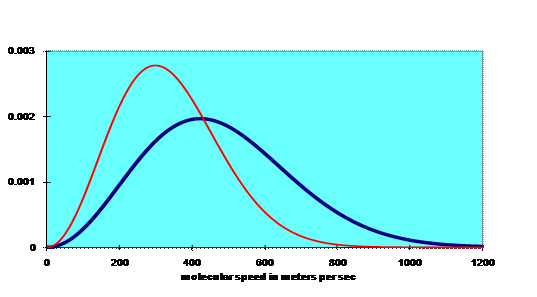
Notice that the number of molecules having high energy drops off fast as the energy increases.  To understand this, think about how a particular molecule gets a high energy.  We now have to deviate from an ideal gas, and consider collisions. The average kinetic energy per molecule is of order kT, so when two molecules collide, energy transfer from one to the other is of this order of magnitude.  Now the collisions are random, so following one particular molecule, it’s just as likely to lose energy as it is to gain it.  This means that to get to a high energy, it must have had a series of lucky collisions, gaining on each one.  The chances of this are similar to the likelihood of getting a string of heads in a row on tossing a coin, which is 2-n for n tosses—another exponential decrease.

Now these rare very fast molecules are very important for planetary science:  the gases in the atmosphere of a planet are those that can be held there by gravity for a long time, billions of years.  But a tiny percentage of the atmosphere’s molecules will sometimes be speeded up beyond escape velocity, and leave the planet.  The crucial question is:  how big is this tiny percentage?   Obviously, it depends on three things:  molecular mass, the temperature of the atmosphere, and the escape velocity.   The important temperature is that up at the edge of the atmosphere.  For Earth, that is about 1500°C, or 1800K.  At that temperature, hydrogen will escape quickly, helium slowly, and oxygen and nitrogen will not escape for all practical purposes.  On the other hand, all of them will escape from the Moon.

The dominant factor in the number of molecules having escape velocity is and in fact since  this factor can be written where ,   using  vrms for the root mean square velocity at the gas temperature.  The average speed of nitrogen molecules at room temperature is about 500 m/sec, so at 1800K (possible upper atmosphere temperature) it would be around 1.2 km/sec. But escape velocity is 11 km/sec, so the fraction is of order exp(-125), no molecules will ever escape. For hydrogen, the same kinetic energy means the v2 is up be a factor of 14, so exp(-125) becomes exp(-9), about one part in eight thousand—the molecules will escape rapidly.  For helium, the factor is exp (-18), they will escape too, but more slowly.